2. 教程: 群体药动学建模#
在本节中，我们将学习如何利用 Masmod 构建简单的群体药动学模型，并学习使用 Notebook 工具。
在开始前，推荐先阅读：Python 编程语言入门、Python 数据科学入门、Markdown 语法。
2.1. 定量药理学和群体药动学#
定量药理学（pharmacometrics）是一门结合传统药理学理论与数学模型而形成的新兴学科，其主要通过建模与模拟的方法来定量描述、阐释和预测药物在人体内的吸收、分布、代谢和排泄的特征、药物在人体内的药效特征及其两者的相关性。
群体药动学（population pharmacokinetics）是定量药理学的重要研究方向之一，与传统的标准两步法（standard two stage）相比，群体药动学利用构建模型的方法来有效整合多个临床研究的数据，在获取药物药动学参数群体典型值及其影响因素的同时，也能通过模型定量诠释药物在体内的药动学特征并进行模拟预测，能大大缩短临床研究所需的人力与时间成本，是模型引导的药物开发（model-informed drug development，MIDD）流程中的应用最广泛也是最关键的技术之一。
备注
若你想了解更多有关于群体药动学的知识，可参考：
若你想了解有关于 MIDD 的内容，可参考：
若你想深入学习群体药动学建模模拟方法，可参考：
焦正. (2019). 基础群体药动学和药效学分析. 科学出版社。
2.2. Notebook 的创建和使用#
我们的 Notebook 参考开源项目 Jupyter Notebook 开发。Jupyter Notebook 相关插件在 VSCode 中的下载量已达上亿数量级，是时下最为流行和便利的数据科学工具之一。
我们软件中的 Notebook 同样提供了这样一个交互式计算平台，允许创建一个包含文本、图形、代码的可交互式文档，为你带来全新的数据分析和建模模拟体验。
下文中我们将先简单学习如何使用软件中的 Notebook。
和新建分析一致，我们可以在新建分析页内选择 “通用 > Notebook” 来创建一个新的 Notebook（图 2.9）。
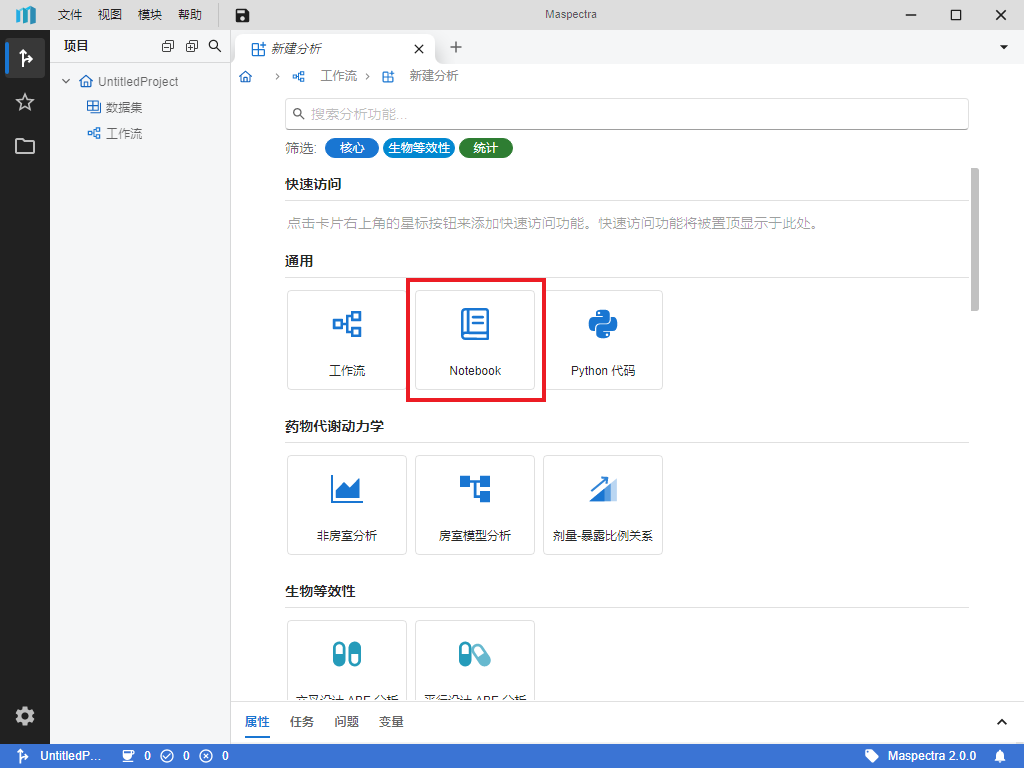
图 2.9 “Notebook” 选项示意图#
在新建的 Notebook 中，我们便可以开始尝试在单元格中输入 Python 代码了。我们试着输入如下代码，并点击左侧的
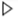按钮以运行代码。运行后，你应该可以看到在单元格下打印出了 “Hello, World!”（图 2.10）。
print("Hello, World!")
Hello, World!
图 2.10 Hello, World! 代码执行后示意图#
我们可以点击标签页顶部工具栏中的 “+ 代码” 按钮来新增一个代码单元格。也可以鼠标悬浮至此单元格下方，点击 “+ 代码” 按钮来新增（图 2.11）。在不处于单元格编辑状态时，也可以按下键盘 B 键来在下方新增一个单元格。接下来你可以在新增的单元格中输入代码并运行，也可以重复几次新增单元格的操作，来熟悉这一流程。
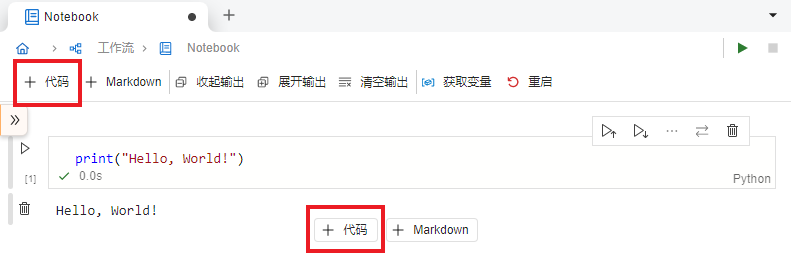
图 2.11 新增代码按钮位置示意图#
小技巧
一些在 Notebook 中常用的键盘快捷键：
A 在 上方 新增一个同类型的单元格（不处于编辑状态时）
B 在 下方 新增一个同类型的单元格（不处于编辑状态时）
Ctrl + Enter 运行代码或完成 Markdown 编辑
2.3. Masmod 入门#
Masmod 是一个基于 Python 编程语言的建模模拟框架，兼容 Python 数据科学生态，力图以最便捷与清晰的方式完成群体建模与模拟的工作流程。
接下来，我们将使用 Masmod 内置的血管内给药一室模型来完成对华法林示例数据集中的血药浓度数据完成群体药动学建模并采用 FOCEi（First Order Conditional Estimation with interaction）算法完成模型拟合。
首先我们需要导入 Masmod 与华法林示例数据，代码如下：
import polars as pl
from mas.model import *
from mas.datasets import warfarin
接下来我们定义一个血管内给药一室模型
Warfarin，同时定义模型中的群体药动学参数（例如清除率和表观分布容积）及其个体间变异：
class WarfarinPk(EvOneCmtLinear.Physio):
def __init__(self) -> None:
""" "定义模型参数"""
super().__init__()
self.tv_cl = theta(0.134, bounds=(0, None))
self.tv_v = theta(7.81, bounds=(0, None))
self.tv_ka = theta(0.571, bounds=(0, None))
self.tv_alag = theta(0.823, bounds=(0, None))
self.eta_cl = omega(0.049)
self.eta_v = omega(0.0802)
self.eta_ka = omega(0.047)
self.eta_alag = omega(0.156)
self.eps_prop = sigma(0.0104)
self.eps_add = sigma(0.554)
def pred(self):
""" "定义模型结构"""
cl = self.tv_cl * exp(self.eta_cl)
v = self.tv_v * exp(self.eta_v)
ka = self.tv_ka * exp(self.eta_ka)
alag = self.tv_alag * exp(self.eta_alag)
F = self.solve(cl=cl, v=v, ka=ka, alag1=alag, s2=v)
ipred = F
y = ipred * (1 + self.eps_prop) + self.eps_add
return y
接着我们筛选出示例数据中的血药浓度数据（即 DVID 不等于 2 的数据）
pk_data = warfarin.filter(pl.col("DVID") != 2)
pk_data.head(10)
| ID | TIME | AMT | DV | DVID | MDV | WT | AGE | SEX | DOSE | EVID |
|---|---|---|---|---|---|---|---|---|---|---|
| i64 | f64 | f64 | f64 | i64 | i64 | f64 | i64 | i64 | f64 | i64 |
| 0 | 0.0 | 100.0 | null | 0 | 1 | 66.7 | 50 | 1 | 100.0 | 1 |
| 0 | 0.5 | null | 0.0 | 1 | 0 | 66.7 | 50 | 1 | 100.0 | 0 |
| 0 | 1.0 | null | 1.9 | 1 | 0 | 66.7 | 50 | 1 | 100.0 | 0 |
| 0 | 2.0 | null | 3.3 | 1 | 0 | 66.7 | 50 | 1 | 100.0 | 0 |
| 0 | 3.0 | null | 6.6 | 1 | 0 | 66.7 | 50 | 1 | 100.0 | 0 |
| 0 | 6.0 | null | 9.1 | 1 | 0 | 66.7 | 50 | 1 | 100.0 | 0 |
| 0 | 9.0 | null | 10.8 | 1 | 0 | 66.7 | 50 | 1 | 100.0 | 0 |
| 0 | 12.0 | null | 8.6 | 1 | 0 | 66.7 | 50 | 1 | 100.0 | 0 |
| 0 | 24.0 | null | 5.6 | 1 | 0 | 66.7 | 50 | 1 | 100.0 | 0 |
| 0 | 36.0 | null | 4.0 | 1 | 0 | 66.7 | 50 | 1 | 100.0 | 0 |
数据筛选完成后，我们就可以将模型与数据结合起来组成群体模型了：
pop_model = PopModel(WarfarinPk, data=pk_data)
[MTran] Start interpreting module: WarfarinPk
[MTran] Interpretation finished in 0.032967 seconds
群体模型定义完成后，我们采用 FOCEi 算法拟合模型：
fit_res = pop_model.fit(FOCEi(print=10))
[MTran] Vaporization started for WarfarinPk(EvOneCmtLinear.Physio)
[MTran] Vaporization finished in 0.195032 seconds
🔧 CXX compiler C:\ProgramData\mingw64\bin\g++.EXE
📦 Compiling build target...
🔗 Linking dynamic library...
✅ Compilation Finished
✈️ First Order Conditional Estimation
Using BFGS...
* maxiter = 9999
* xtol = 1e-06
* ftol = 1e-06
* lower_bounds =
* upper_bounds =
* log_level = 0
* print = 10
* print_type = 0
* verbose = 1
* p_small = 0.1
* rel_step_size = 0.001
# 0 ofv: 347.7917575
Params: 1.0000e-01 1.0000e-01 1.0000e-01 1.0000e-01 1.0000e-01 1.0000e-01 1.0000e-01 1.0000e-01 1.0000e-01 1.0000e-01
NParams: 1.3400e-01 7.8100e+00 5.7100e-01 8.2300e-01 2.2136e-01 2.8320e-01 2.1679e-01 3.9497e-01 1.0198e-01 7.4431e-01
Gradients: -1.0509e+01 -8.3374e+00 -9.6925e+01 3.0800e+01 -2.7513e+01 1.7544e+01 -3.3121e+01 -1.1511e+01 4.3184e+01 1.2218e+02
Funcalls: 8
# 1 ofv: 252.9367071
Params: 1.5161e-01 1.4094e-01 5.7596e-01 -5.1245e-02 2.3511e-01 1.3849e-02 2.6265e-01 1.5653e-01 -1.1206e-01 -5.0000e-01
NParams: 1.4110e-01 8.1364e+00 9.1906e-01 7.0748e-01 2.5338e-01 2.5982e-01 2.5509e-01 4.1794e-01 8.2493e-02 4.0849e-01
Gradients: 5.8501e+01 1.9482e+01 -1.2655e+01 4.3841e-01 -2.0968e+01 1.4030e+01 -3.3114e+01 -4.1979e+00 7.4639e+00 4.2037e+01
Funcalls: 17
# 11 ofv: 219.1455277
Params: 6.6128e-02 1.1409e-01 1.1174e+00 1.3436e-01 3.6191e-01 -1.8678e-01 1.6618e+00 -3.4404e-02 -4.8287e-02 -1.0445e+00
NParams: 1.2954e-01 7.9209e+00 1.5794e+00 8.5177e-01 2.8764e-01 2.1259e-01 1.0336e+00 3.4530e-01 8.7926e-02 2.3697e-01
Gradients: -1.2234e+01 -8.0065e+00 1.1216e+00 2.0787e+00 -3.1722e-01 -3.4493e+00 4.2760e+00 -2.3902e+00 -2.9918e+00 -5.9325e+00
Funcalls: 109
# 21 ofv: 218.0048633
Params: 8.5523e-02 1.2083e-01 9.4660e-01 8.7367e-02 3.6555e-01 -1.5218e-01 1.4398e+00 1.1198e-01 -6.5216e-02 -9.5924e-01
NParams: 1.3207e-01 7.9744e+00 1.3314e+00 8.1267e-01 2.8868e-01 2.2007e-01 8.2776e-01 3.9973e-01 8.6450e-02 2.5807e-01
Gradients: -4.2353e-01 -4.2524e-01 -2.0438e-01 -7.2524e-01 -6.3465e-02 -7.3090e-02 -5.6033e-02 -2.5406e-02 1.8580e-02 -1.1706e-01
Funcalls: 223
converged = True
n_iter = 25
x_opt = 8.6104e-02 1.2128e-01 9.6344e-01 1.0153e-01 3.6619e-01 -1.5174e-01 1.4490e+00 9.8417e-02 -6.5853e-02 -9.5697e-01
f_opt = 217.9974593
fun_calls = 281
Estimation Summary
────────────────────────────────────────────────────────────────────────────────
Step OFV
────────────────────────────────────────────────────────────────────────────────
✅ Converged 217.997
────────────────────────────────────────────────────────────────────────────────
Parameter Estimation
────────────────────────────────────────────────────────────────────────────────
Parameter Estimate Shrinkage(%)
────────────────────────────────────────────────────────────────────────────────
Theta
tv_cl 0.132
tv_v 7.978
tv_ka 1.354
tv_alag 0.824
Omega(SD)
eta_cl 0.289 0.000
eta_v 0.220 3.994
eta_ka 0.835 50.450
eta_alag 0.394 59.243
Sigma(SD)
eps_prop 0.086 14.953
eps_add 0.259 15.636
────────────────────────────────────────────────────────────────────────────────
Information
────────────────────────────────────────────────────────────────────────────────
Number of Time
Iterations
────────────────────────────────────────────────────────────────────────────────
25 0:00:01.74
────────────────────────────────────────────────────────────────────────────────
Estimation finished, now start covariance calculation.
Computing Covariance...
Covariance computation succeed
最后，我们来查看模型拟合结果：
fit_res
Estimation Summary
| Estimation | Covariance | OFV |
|---|---|---|
| ✅ Converged | ✅ Succeed | 217.997 |
| Number of Observations: | 250 | |
| Number of Parameters: | 10 | |
Parameter Estimation
| Parameter | Estimate | RSE(%) | Shrinkage(%) |
|---|---|---|---|
| Theta | |||
| tv_cl | 0.132 | 5.218 | |
| tv_v | 7.978 | 4.075 | |
| tv_ka | 1.354 | 31.875 | |
| tv_alag | 0.824 | 19.042 | |
| Omega(SD) | |||
| eta_cl | 0.289 | 14.184 | 0.000 |
| eta_v | 0.220 | 13.348 | 3.994 |
| eta_ka | 0.835 | 19.140 | 50.450 |
| eta_alag | 0.394 | 28.390 | 59.243 |
| Sigma(SD) | |||
| eps_prop | 0.086 | 14.235 | 14.953 |
| eps_add | 0.259 | 23.629 | 15.636 |
Information
| Number of Iterations | Time | ||
|---|---|---|---|
| Compilation | Estimation | Covariance | |
| 25 | 0:00:00.20 | 0:00:01.74 | 0:00:04.32 |