Cox 回归分析#

使用软件内的 “Cox 回归分析” 可以对生存数据建立 Cox 回归模型（Cox regression model）来探索各个协变量因素对风险率的影响。

数据映射关系#

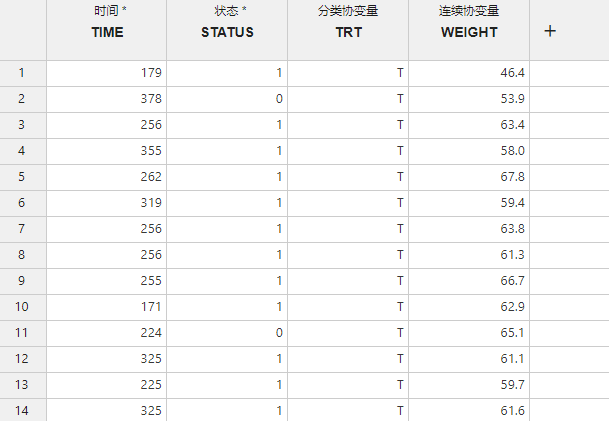
../../_images/stats-cox-mapping.png

图 505 Cox 回归分析数据映射示意图#

  • 时间 （必选项，单选）：研究对象存活时间。

  • 状态 （必选项，单选）：研究对象的状态，指代是否发生事件或删失。

  • 连续协变量（可选项，多选）：Cox 回归模型中的连续型协变量。

  • 分类协变量（可选项，多选）：Cox 回归模型中的分类型协变量。对于此类变量，将分别计算各个分类的回归系数。

分析选项#

数据选项#

../../_images/stats-cox-option-data.png

图 506 数据选项示意图#

  • 事件定义：指定 “状态” 数据中代表事件发生的标识值。除此以外的标识值将均指代删失。可选项为 “状态” 数据中所有不重复的数据值。默认值为其中首个数据值。

模型选项#

../../_images/stats-cox-option-model.png

图 507 模型选项示意图#

在此选项内的输入框内输入 Cox 回归模型需要考察的协变量，由 “连续协变量” 或 “分类协变量” 的列名以及加号（+）组成。也即 Cox 回归模型 \(h(t | X_i) = h_0(t) exp(\beta_1 X_{i1} + \beta_2 X_{i2} + \cdots + \beta_p X_{ip})\) 中 \(X_{i1}, X_{i2}, \cdots, X_{ip}\) 的部分。向量 \(X_i = (X_{i1}, X_{i2}, \cdots, X_{ip})\) 取值于数据集中与其同名的数据列。

例如对于以下数据（图 531）：

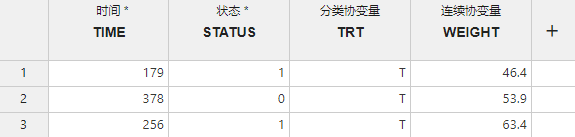
../../_images/stats-cox-option-model-example-data.png

图 508 模型选项数据示例#

在 “模型选项” 内输入以下自变量组合形式：TRT + WEIGHT（图 509），此时事件发生时间为 378 的个体对应的 \(X = (T, 53.9)\)。

../../_images/stats-cox-option-model-example-formula.png

图 509 模型选项公式示例#

计算选项#

../../_images/stats-cox-option-calc.png

图 510 模型选项示意图#

  • 风险比置信区间 (%)：设置风险比（hazard ratio）置信区间的置信水平。例如输入 95 即计算风险比的 95% 置信区间。风险比即 \(exp(\beta)\)，\(\beta\) 为回归系数，详情可参见 Cox 回归模型假设与基本形式 小节。默认值为 95。

分析结果#

分析选项#

本次 Cox 回归分析的模型形式与分析选项设置。示例可见 图 511。

../../_images/stats-cox-result-options.png

图 511 分析选项表格示意图#

参数估计#

Cox 回归模型的回归系数以及风险比估算结果。详细的参数估计流程可见 模型参数估计 小节。示例可见 图 512。

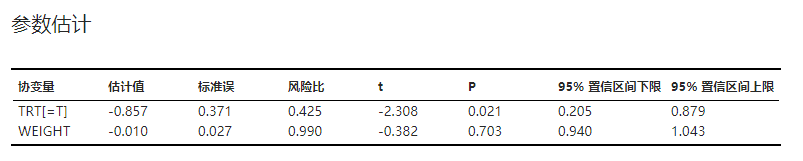
../../_images/stats-cox-result-estimates.png

图 512 参数估计表格示意图#

模型诊断#

模型诊断信息表格，包含目标函数值（-2 倍的对数似然函数值，即 “-2LL” 列）、AIC（赤池信息准则，Akaike information criterion） 与 BIC（贝叶斯信息准则，Bayesian Information Criterion）。示例可见 图 513。

../../_images/stats-cox-result-model-check.png

图 513 模型诊断表格示意图#

运行日志#

Cox 回归分析的运行日志，包含软件版本、运行时间、模型拟合成功与否等信息。示例可见 图 514。

../../_images/stats-cox-result-log.png

图 514 运行日志示意图#

统计理论#

模型假设与基本形式#

在生存分析中，研究者通常感兴趣的是协变量 \(X\) 与生存函数 \(S(t, X)\) 之间的关系。容易想到，我们可以使用线性回归的方法来解决这一问题，但是由于删失数据的存在以及时间变量往往不符合正态分布，导致了传统线性回归方法在生存分析中难以施展拳脚。

而 Cox 回归模型以风险函数 \(h(t, X)\) 作为因变量，模型基本形式如下：

\[\begin{split} h(t | X_i) & = h_0(t) exp(\beta_1 X_{i1} + \beta_2 X_{i2} + \cdots + \beta_p X_{ip}) \\ & = h_0(t) exp(\beta \cdot X_i) \end{split}\]

其中 \(X_i = (X_{i1}, X_{i2}, \cdots, X_{ip})\) 代表样本 \(i\) 的 \(p\) 个协变量的观测值；\(h(t | X_i)\) 为 \(t\) 时刻下且协变量值为 \(X_i\) 时对应的风险率；\(h_0(t)\) 为基础风险函数；\(\beta = (\beta_{1}, \beta_{2}, \cdots, \beta_{p})\) 为各个协变量对应的回归系数，反映了协变量对风险率影响的大小。

此时若将两个风险率相除（得到的比例被称为风险比）则可以得到它们之间相对的风险程度大小。例如对于样本 \(i\) 与 \(j\)：

\[\begin{split} \frac{h(t | X_i)}{h(t | X_j)} &= \frac{h_0(t) exp(\beta \cdot X_i)}{h_0(t) exp(\beta \cdot X_j)} \\ &= \frac{exp(\beta \cdot X_i)}{exp(\beta \cdot X_j)} \\ &= exp[\beta \cdot (X_i - X_j)] \end{split}\]

通过以上例子，我们可以总结 Cox 回归模型的如下特点：

  1. 不对基础风险函数 \(h_0(t)\) 的形式做任何假设，但认为其不随样本的变化而变化，从而可通过风险比的形式免去了对其的估算。

  2. 协变量效应与对数基础风险函数呈线性关系，且效应大小不随时间变化，使得风险比值为常数（因此 Cox 回归模型也被称为比例风险模型，proportional hazards model）。

此外，与传统的线性回归模型不同，Cox 回归模型不包含截距项。若包含截距项 \(\beta_0\)，则模型形式将变为：

\[\begin{split} h(t | X_i) & = h_0(t) exp(\beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \cdots + \beta_p X_{ip}) \\ & = [exp(\beta_0)h_0(t)] exp(\beta \cdot X_i) \end{split}\]

可以看到，\(exp(\beta_0)h_0(t)\) 其实也可以被视作基础风险函数。因而原模型形式中的 \(h_0(t)\) 已包含了所有与协变量无关的风险率，不需要额外的截距项。

模型参数估计#

假设共发生 \(n\) 次事件，对应的存活时间为 \(t_n\)，且有 \(t_1 < t_2 < \cdots < t_n\)。则在 \(t_i\) 时刻，某个体发生事件的概率为：

\[ \frac{exp(\beta \cdot X_i)}{\sum_{j: t_j ≥ t_i} exp(\beta \cdot X_j)} = \frac{\theta_i}{\sum_{j: t_j ≥ t_i} \theta_j} \]

其中 \(\theta_i = exp(\beta \cdot X_i)\)；\(t_j\) 为在 \(t_i\) 时刻仍存活的个体的存活时间。因此对于所有事件，其似然函数可以写为：

\[ L(\beta) = \prod \limits_{i=1}^n \frac{\theta_i}{\sum_{j: t_j ≥ t_i} \theta_j} \]

小技巧

用概率的形式可以更好的理解以上公式：

\[ P(t_1 < t_2 < \cdots < t_n) = \frac{\theta_1}{\theta_1 + \theta_2 + \cdots \theta_n} \times \frac{\theta_2}{\theta_2 + \cdots \theta_n} \times \cdots \times \frac{\theta_n}{\theta_n} \]

对数似然为：

\[ \mathscr{l}(\beta) = \sum_{i=1}^n (\beta \cdot X_i - log \sum_{j: t_j ≥ t_i} \theta_j) \]

其梯度为：

\[ \mathscr{l}'(\beta) = \sum_{i=1}^n (X_i - \frac{\sum_{j: t_j ≥ t_i} \theta_j X_j}{\sum_{j: t_j ≥ t_i} \theta_j}) \]

参考文献

Cox, B. D. R. . (1972). Regression models and life-tables. Journal of the Royal Statal Society, 34(2).

知晓梯度后，我们便可以使用各种优化算法（例如牛顿逼近法）来求取 \(\beta\) 的最大似然估计值。

我们也可以对回归系数估计值进行假设检验来探索其对风险率是否有显著的解释作用，相关检验方法可详见：线性回归模型回归系数的检验。

扩展阅读

当事件发生时间出现重合（ties）时的处理方法：

  • Efron, B. . (1977). The efficiency of cox's likelihood function for censored data. JASA: Journal of the American Statistical Association, 72(359), 557-565.

对随时间变化的协变量效应（time-dependent covariates）进行分析：

  • Martinussen, T. , & Scheike, T. H. . (2006). Dynamic regression models for survival data. Springer.

对协变量模型进行筛选：

  • Tibshirani R. (1997). The lasso method for variable selection in the Cox model. Statistics in medicine, 16(4), 385–395.

案例#

我们现有一组术后胃癌患者的生存数据（数据如下所示），其中记录了患者存活时间 TIME、患者状态 STATUS（1 为事件发生，0 为删失）、年龄 AGE 与性别 SEX，我们欲通过 Cox 回归模型来分析不同性别以及不同年龄的胃癌患者的风险比。

TIME	STATUS	AGE	SEX

118	1	70	Male
144	1	67	Female
166	0	61	Male
170	1	57	Female
210	1	57	Male
218	1	53	Male
301	1	67	Male
306	0	74	Male
310	1	68	Female
361	1	71	Female
371	1	58	Male
390	1	53	Male
394	1	72	Female
455	1	68	Male
520	1	70	Female
567	1	57	Male
574	1	60	Male
613	0	70	Male
624	1	50	Male
654	1	68	Female
707	1	63	Male
728	1	68	Female
883	1	60	Male
925	1	55	Female

  1. 新建一个 “Cox 回归分析”，在 时间、状态、连续协变量 及 分类协变量 列内分别输入上述数据，如 图 515 所示：

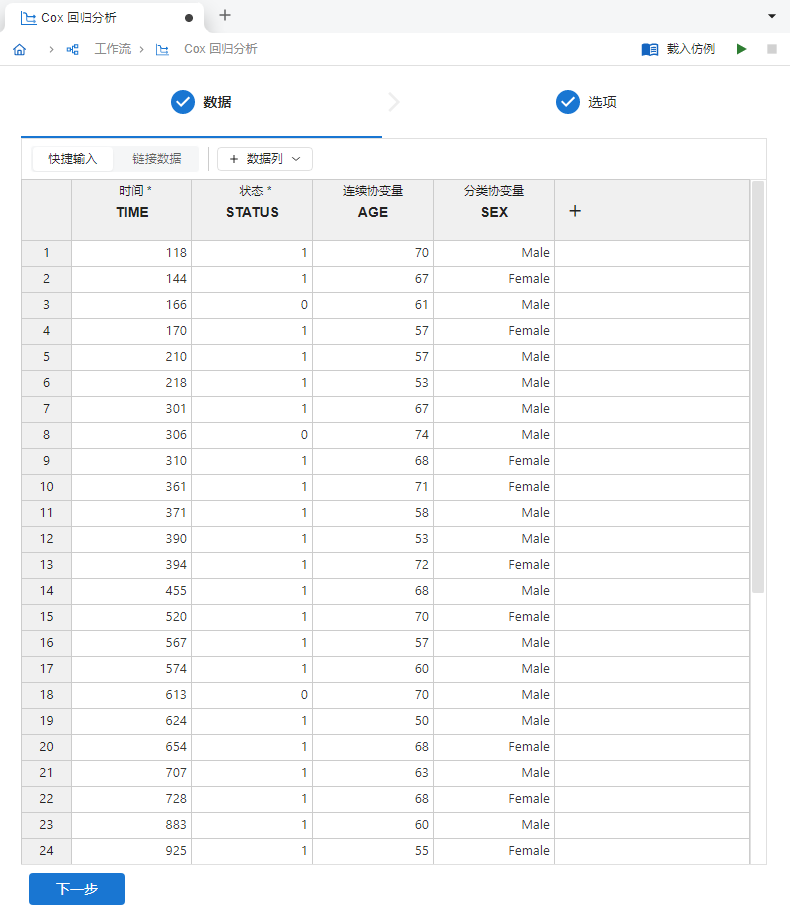
../../_images/stats-cox-example-data.png

图 515 输入数据示意图#

  1. 输入完成后，点击 “下一步” 按钮进入选项页。修改 “事件定义” 为 1；“模型公式” 为 AGE + SEX，如 图 516 所示：

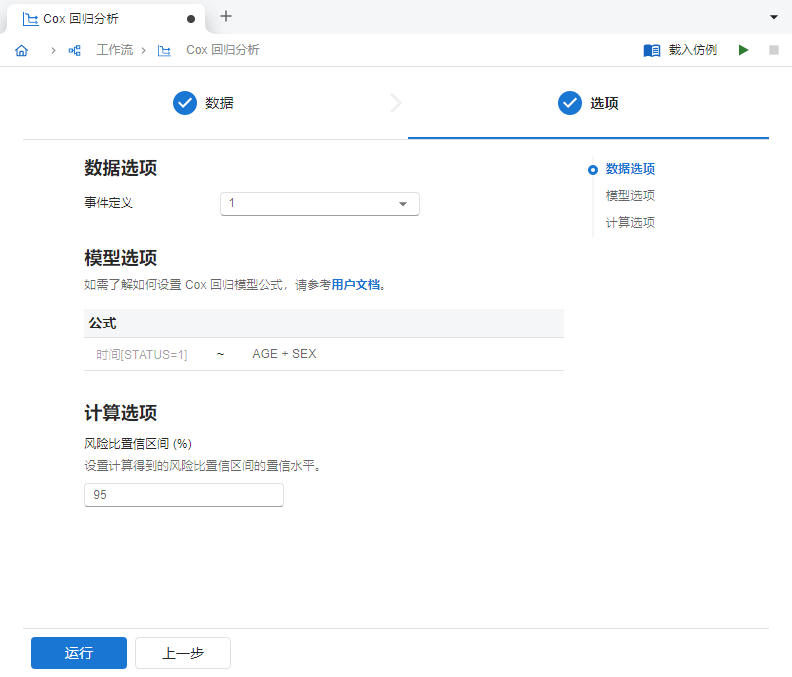
../../_images/stats-cox-example-options.png

图 516 分析选项示意图#

  1. 选项设置完成后，点击 “运行” 按钮执行 Cox 回归分析。在结果的 “参数估计” 表格（图 517）中，我们可以获知协变量回归系数估计值分别为 0.020 与 0.191，因此可写出以下公式：

\[\begin{split} \frac{h(t|AGE = 70)}{h(t|AGE = 50)} = \frac{exp(0.020 \times 70)}{exp(0.020 \times 50)} ≈ 1.49 \\ \end{split}\]
\[ \frac{h(t|SEX = Male)}{h(t|SEX = Female)} = exp(0.191) ≈ 1.21 \]

即若患者年龄分别为 70 岁与 50 岁，则 70 岁患者的风险率是 50 岁患者的 1.49 倍。而男性患者的风险率是女性患者的 1.21 倍。

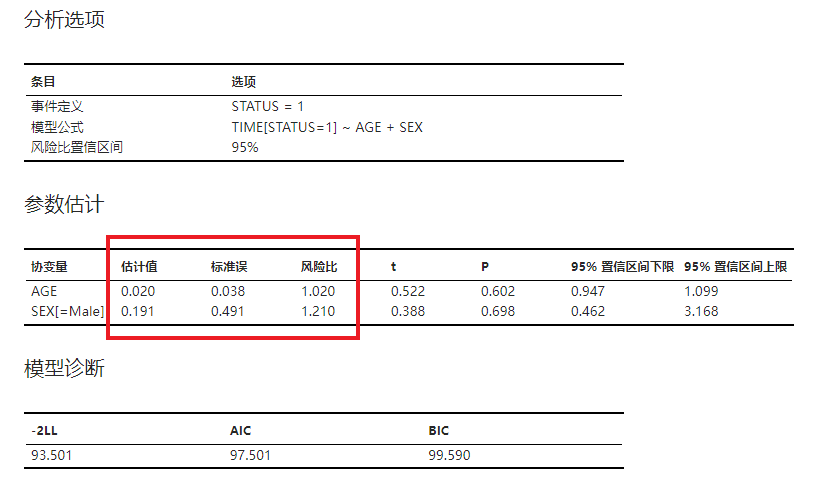
../../_images/stats-cox-example-results.png

图 517 分析结果表格示意图#