3.2. 交叉表卡方分析#
使用软件的 “交叉表卡方分析” 功能,可通过交叉表统计两个变量内各个分类出现的频率并进行独立性卡方检验(chi-square test)以确定两个变量间是否有关联性。
3.2.1. 数据映射关系#
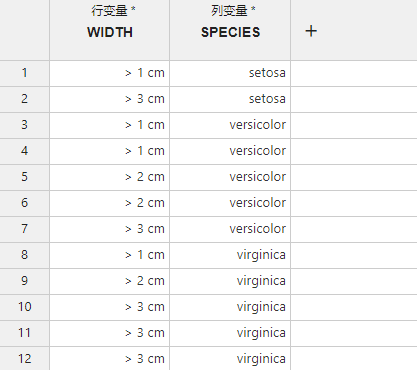
图 3.122 交叉表卡方分析数据映射示意图#
行变量 (必选项,多选):需要统计各分类频数并作为 2x2 交叉表行分类的变量数据。
列变量 (必选项,多选):需要统计各分类频数并作为 2x2 交叉表列分类的变量数据。
备注
如果同时存在多个行变量或列变量,将依次两两组成交叉表并进行分析。
3.2.2. 分析选项#
计算选项#
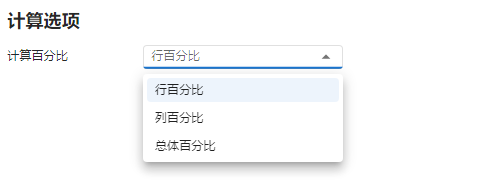
图 3.123 计算选项示意图#
计算百分比:选择是否需要计算当前分类内的个体在当前行/列/总体中的百分比。可选项包括
行百分比、列百分比与总体百分比。默认值为行百分比。
3.2.3. 分析结果#
分析选项#
本次交叉表卡方分析的分析选项设置。示例可见 图 3.124。

图 3.124 分析选项表格示意图#
实测频数#
行变量与列变量各个分类内个体的实测频数。示例可见 图 3.125。
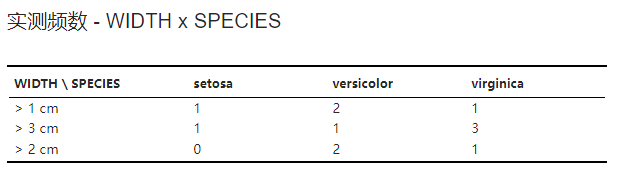
图 3.125 实测频数表格示意图#
期望频数#
行变量与列变量各个分类内个体的期望频数。计算方法可参考下方统计理论内的 交叉表卡方分析 小节。示例可见 图 3.126。
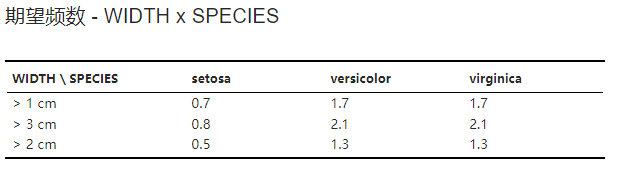
图 3.126 期望频数表格示意图#
行百分比/列百分比/总体百分比#
当前分类内的个体在当前行/列/总体中的百分比。具体表格内容由 计算选项 中的 “计算百分比” 选项控制。示例可见 图 3.127。
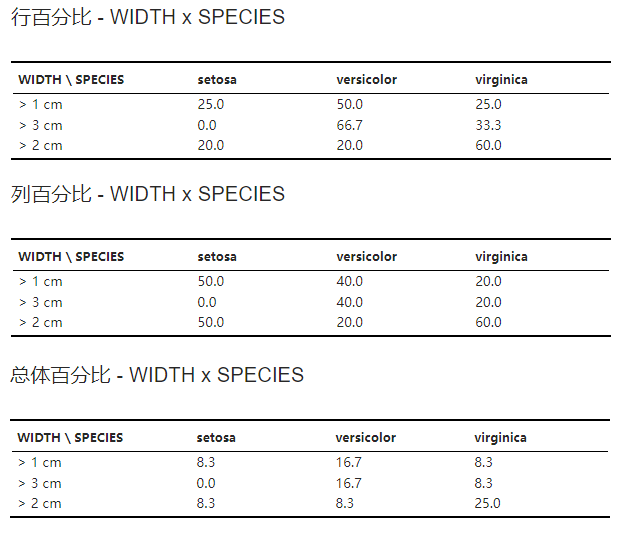
图 3.127 行百分比/列百分比/总体百分比表格示意图#
卡方检验#
交叉表卡方检验结果,包括统计量 \(\chi^2\) 与对应的 P 值。统计量的计算方法可参考下方的 交叉表卡方分析 小节。示例可见 图 3.128。

图 3.128 卡方检验表格示意图#
运行日志#
交叉表卡方分析的运行日志,包含软件版本、运行时间、运行成功与否等信息。示例可见 图 3.129。

图 3.129 运行日志示意图#
3.2.4. 统计理论#
卡方分布#
设随机变量 \(X_1, X_2, \cdots, X_n\) 独立同分布于标准正态分布 \(N(0, 1)\),则 \(\chi^2 = X_1^2 + X_2^2 + \cdots + X_n^2\) 的分布称为自由度为 \(n\) 的 \(\chi^2\) 分布(一般读作卡方分布),记作 \(\chi^2 \sim \chi^2(n)\)。
\(\chi^2\) 分布的期望 \(E(\chi^2) = n\),方差 \(Var(\chi^2)=2n\)。不同自由度下的 \(\chi^2\) 分布概率密度函数如 图 3.130 所示。
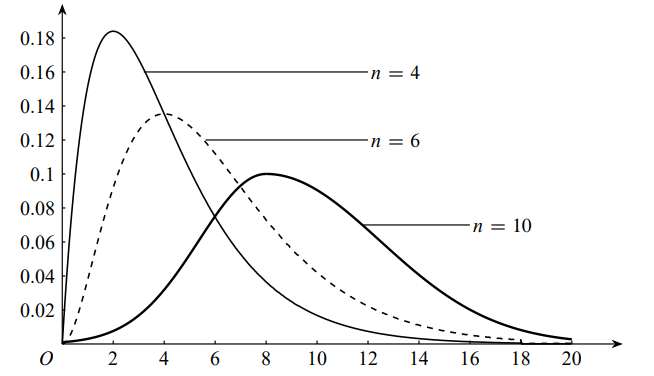
图 3.130 卡方分布概率密度函数示意图#
来源:茆诗松, 程依明, & 濮晓龙. (2019). 概率论与数理统计教程(第三版). 高等教育出版社.
交叉表卡方分析#
交叉表是将观测数据按两个或更多属性分类时所列出的频数表(频数的定义请参考:频数与频率),例如将 1000 名受试者按是否吸烟以及是否罹患肺癌进行分类可得到如下的交叉表:
是否患癌/是否吸烟 |
是 |
否 |
行和 |
|---|---|---|---|
是 |
539 |
288 |
827 |
否 |
72 |
101 |
173 |
列和 |
640 |
360 |
1000 |
交叉表一般分析的问题是考察各个属性之间是否有关联性,也即判断表中的两类属性是否独立。例如对于上表,我们想分析的问题为受试者是否患癌与其吸烟是否相关。
用统计语言来表述的话,交叉表卡方分析的原假设为:\(p_{ij} = p_{i\cdot} \times p_{\cdot j}\);备择假设为:\(p_{ij} \neq p_{i\cdot} \times p_{\cdot j}\) 。
其中,\(p_{i\cdot}\)、\(p_{\cdot j}\)、\(p_{ij}\) 分别表示在 \(r \times c\) 交叉表(如下表)中一个个体仅属于分类 \(A_i\)、仅属于分类 \(B_j\) 和同时属于 \(A_i\) 与 \(B_j\) 的概率。
\(A\) / \(B\) |
\(1\) |
\(\cdots\) |
\(j\) |
\(\cdots\) |
\(c\) |
行和 |
|---|---|---|---|---|---|---|
\(1\) |
\(p_{11}\) |
\(\cdots\) |
\(p_{1j}\) |
\(\cdots\) |
\(p_{1c}\) |
\(p_{1\cdot}\) |
\(\vdots\) |
\(\vdots\) |
\(\vdots\) |
\(\vdots\) |
\(\vdots\) |
||
\(i\) |
\(p_{i1}\) |
\(\cdots\) |
\(p_{ij}\) |
\(\cdots\) |
\(p_{ic}\) |
\(p_{i\cdot}\) |
\(\vdots\) |
\(\vdots\) |
\(\vdots\) |
\(\vdots\) |
\(\vdots\) |
||
\(r\) |
\(p_{r1}\) |
\(\cdots\) |
\(p_{rj}\) |
\(\cdots\) |
\(p_{rc}\) |
\(p_{r\cdot}\) |
列和 |
\(p_{\cdot 1}\) |
\(\cdots\) |
\(p_{\cdot j}\) |
\(\cdots\) |
\(p_{\cdot c}\) |
\(1\) |
对于同时属于分类 \(A_i\) 与 \(B_j\) 的个体出现的频率 \(n_{ij}/n\) 应当与概率 \(p_{ij} = p_{i\cdot} \times p_{\cdot j}\) 较为接近时才能使原假设成立;或者说其实际频数 \(n_{ij}\) 与理论频数 \(n p_{ij}\) 应当较为接近。所以我们可以构造如下统计量:
此统计量近似服从于自由度为 \((r-1)(c-1)\) 的 \(\chi^2\) 分布(证明过程请见下方参考文献)。
其中 \(\hat{p_{ij}}\) 为 \(p_{ij}\) 的最大后验估计值,\(\hat{p_{ij}} = \hat{p_{i\cdot}} \cdot \hat{p_{\cdot j}} = \frac{n_{i \cdot}}{n} \cdot \frac{n_{\cdot j}}{n}\)。\(n \hat{p_{ij}}\) 一般也被称为期望频数。
若假设检验显著性水平为 \(\alpha\),当 \(\chi^2 > \chi^2_{1 - \alpha}((r-1)(c-1))\) 时则拒绝原假设,认为两属性有关联,否则接受原假设。
参考文献
R. A. Fisher. (1935). The Design of Experiments. Oliver and Boyd.
3.2.5. 案例#
例如我们有一份数据(如下表),包含了 20 名受试者是否吸烟与是否患肺癌的情况,我们欲分析肺癌患病与吸烟是否有关联性。我们可以使用交叉表卡方分析功能来完成上述分析。
是否吸烟 是否患癌
是 是
是 是
是 是
否 否
否 是
是 是
是 是
是 是
否 否
是 否
是 是
是 是
否 否
否 否
否 是
是 是
是 是
是 是
是 是
否 否
新建一个 “交叉表卡方分析”,并在
行变量与列变量内分别输入上述数据,如 图 3.131 所示:
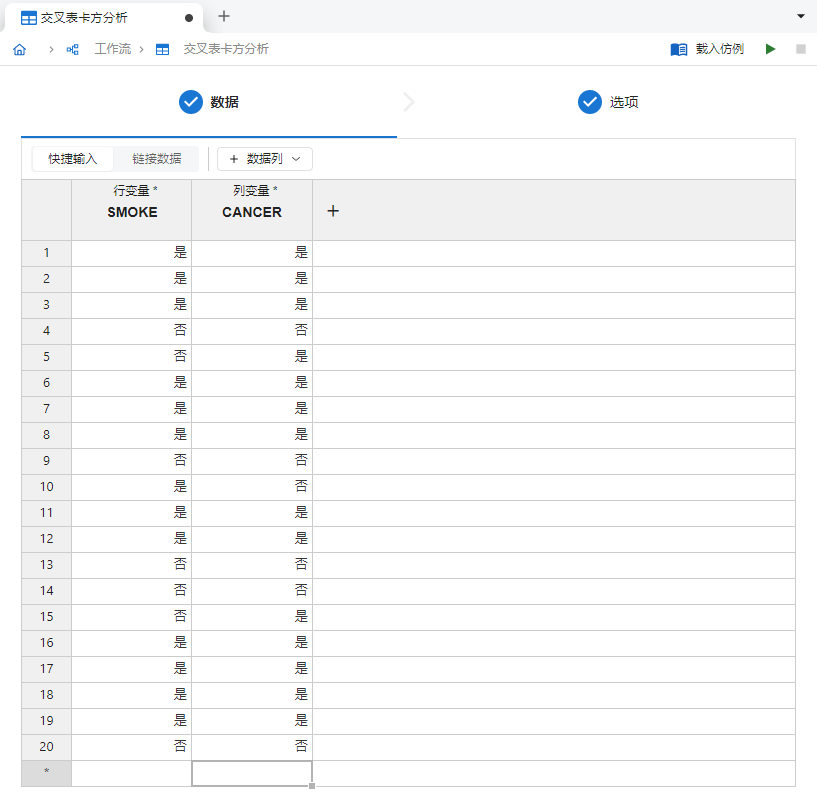
图 3.131 输入数据示意图#
输入完成后,点击 “下一步” 按钮,可在计算选项中选择
总体百分比(图 3.132)以获知各个分类内个体的占比情况。
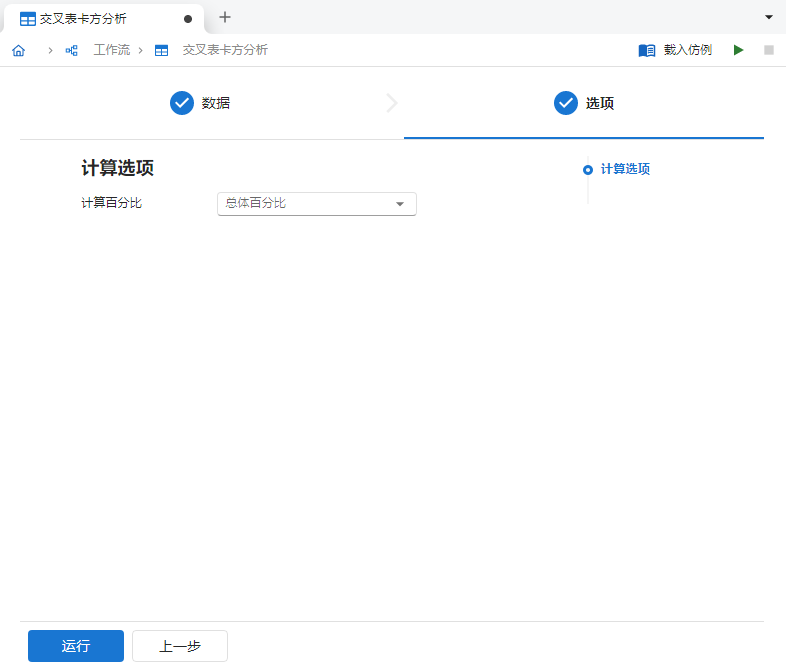
图 3.132 计算选项设置示意图#
设置完成后,点击 “运行” 按钮以执行分析。在结果中可以查看由行变量以及列变量组成的交叉表与各个分类内个体出现的频数;在 “卡方检验” 表格(图 3.133)中则可以查看计算的统计量与对应的 P 值。本例数据的 P 值为 0.014,因此我们可以认为患肺癌与吸烟之间有较强的相关性。
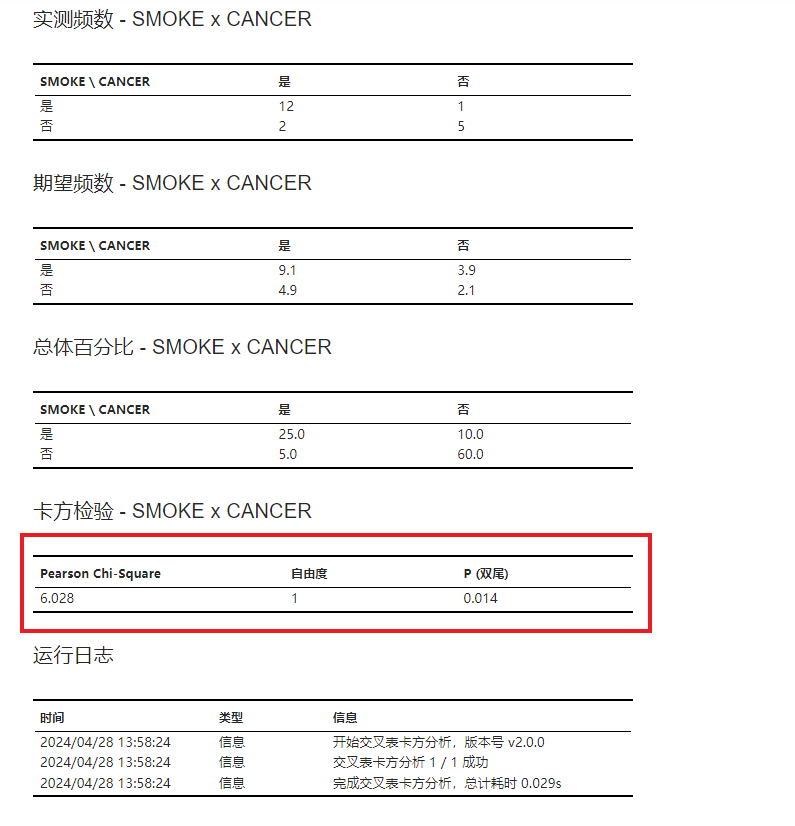
图 3.133 卡方分析结果示意图#
