双样本 t 检验#

通过软件内的 “双样本 t 检验” 功能，可以对两组独立的样本数据进行双样本 t 检验（two-sample t-test）。

双样本 t 检验一般用于检验两组独立且符合正态分布的数据的均值是否相等。

数据映射关系#

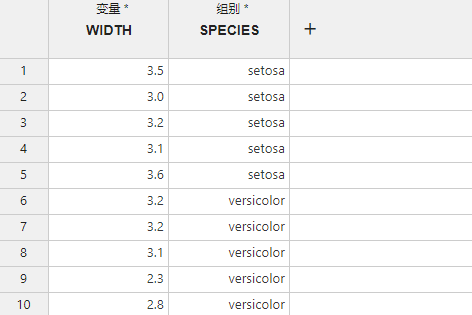
../../_images/stats-two-sample-t-mapping.png

图 431 双样本 t 检验数据映射示意图#

  • 变量 （必选项，多选）：需要检验的变量数据。若有多个变量，则将分别进行检验。

  • 组别 （必选项，单选）：组别数据。用于区分变量数据所属的组别，拥有相同组别值的变量数据将被视作同一组。

分析选项#

组别定义#

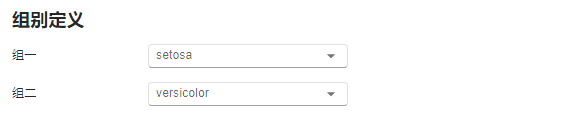
../../_images/stats-two-sample-t-option-group.png

图 432 组别定义选项示意图#

  • 组一：定义第一组数据的组别值。默认值为组别数据中出现的第一个不重复的字符串。

  • 组二：定义第二组数据的组别值。默认值为组别数据中出现的第二个不重复的字符串。

计算选项#

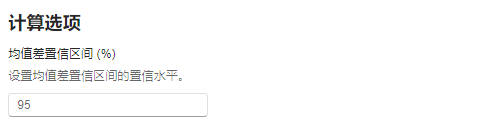
../../_images/stats-two-sample-t-option-calc.png

图 433 计算选项示意图#

  • 均值差置信区间（%）：均值差置信区间的置信水平。默认值为 95。计算方法如下：

均值差置信区间计算方法

设第一组、第二组数据的均值分别为 \(\bar X_1\) 与 \(\bar X_2\)，均值差计算方法为：

\[MeanDiff = \bar X_1 - \bar X_2\]

记输入的置信水平为 \(P\)，则均值差置信区间 \(CI\) 计算方法如下：

\[P = (1 - \alpha) \times 100\%\]
\[CI = MeanDiff \pm [t_{1 - \frac{\alpha}{2}, df} \times SE(MeanDiff)]\]

其中 t 分布的自由度 \(df\) 将因方差齐性假设的不同而不同，具体计算方法可详见 统计理论。

假定等方差时：

\[SE(MeanDiff) = \sqrt{\frac{\sum_{i=1}^{N_1}(X_{1i} - \bar{X_1})^2 + \sum_{i=1}^{N_2}(X_{2i} - \bar{X_2})^2}{N_1 + N_2 - 2} (\frac{1}{N_1} + \frac{1}{N_2})}\]

不假定等方差时：

\[SE(MeanDiff) = \sqrt{\frac{(SD(X_1))^2}{N_1} + \frac{(SD(X_2))^2}{N_2}}\]

分析结果#

分析选项#

本次双样本 t 检验的分析选项设置。示例可见 图 434。

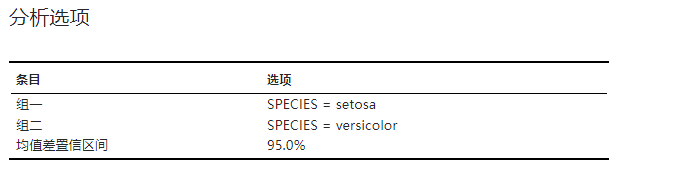
../../_images/stats-two-sample-t-result-options.png

图 434 分析选项表格示意图#

描述性统计#

各组数据以及全部数据的描述性统计结果，包括均值、标准差、中位数等。示例可见 图 435。

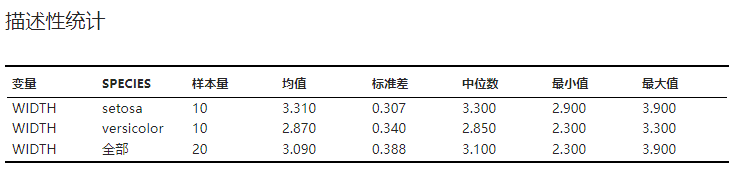
../../_images/stats-two-sample-t-result-des-results.png

图 435 描述性统计表格示意图#

独立双样本 t 检验#

双样本 t 检验结果，包括在不同方差齐性假设下的均值差、统计量 t 值及假设检验 P 值等结果。示例可见 图 436。

Levene's 方差齐性检验相关内容可见：Levene's 检验。

../../_images/stats-two-sample-t-result-test-results.png

图 436 独立双样本 t 检验表格示意图#

运行日志#

双样本 t 检验运行日志，包含软件版本、运行时间、运行成功与否等信息。示例可见 图 437。

../../_images/stats-two-sample-t-result-log.png

图 437 运行日志示意图#

统计理论#

独立双样本 t 检验#

双侧独立双样本 t 检验的原假设为：两组样本均值 \(\bar X_1\) 与 \(\bar X_2\) 相等；

其备择假设为：两组样本均值 \(\bar X_1\) 与 \(\bar X_2\) 不相等；

计算的统计量为 \(t\)，在假定等方差时的计算公式为：

\[ s_p^2 = \frac{(N_1 - 1) S_1^2 + (N_2 - 1)S_2^2}{N_1 + N_2 - 2} \]
\[ t = \frac{\bar{X_1} - \bar{X_2}}{s_p \sqrt{\frac{1}{N_1} + \frac{1}{N_2}}} \]

其中 \(S_1^2\)、\(S_2^2\) 分别为第一组与第二组数据的标准差。

在不假定等方差时，\(t\) 值计算公式如下：

\[ t = \frac{\bar{X_1} - \bar{X_2}}{\sqrt{\frac{S_1^2}{N_1} + \frac{S_2^2}{N_2}}} \]

若假设检验置信水平为 \(\alpha\)，自由度为 \(df\)（计算公式见下文），在双侧检验时记 t 分布中界值为 \(t_{\frac{\alpha}{2}, df}\)。当 \(|t| > t_{1 - \frac{\alpha}{2}, df} \) 时则拒绝原假设，认为两组样本均值 \(\bar X_1\) 与 \(\bar X_2\) 不等，否则接受原假设。

双样本 t 检验自由度计算方法

假定等方差时：

\[df = N_1 + N_2 - 2。\]

不假定等方差时：

\[df = \frac{\left(\frac{S_1^2}{N_1} + \frac{S_2^2}{N_2}\right)^2}{\frac{(\frac{S_1^2}{N_1})^2}{N_1 - 1} + \frac{(\frac{S_2^2}{N_2})^2}{N_2 - 1}}\]

Levene's 检验#

在使用软件进行双样本 t 检验时，在假定等方差时将对两组数据额外进行一次 Levene's 检验以证明方差齐性。

Levene's 检验原假设为：各组间方差相等；备择假设为：各组间方差不相等。

假设总样本量为 \(N\)，其中共有 \(k\) 组数据，每组中样本量为 \(n_k\)，第 \(i\) 组的第 \(j\) 个观测值记为 \(X_{ij}\)，第 \(i\) 组均值记作 \(\bar{X_i}\)。Levene's 检验统计量 \(F\) 的计算方法为：

\[ d_{ij} = |X_{ij} - \bar{X_i}| \]
\[ D_i = \frac{1}{n_i} \sum_{j = 1}^{n_i}d_{ij} \]
\[ \bar D = \frac{1}{k} \sum_{i = 1}^{k}D_{i} \]
\[ F = \frac{N-k}{k-1} \frac{\sum_{i = 1}^{k}n_i(D_i - \bar{D})^2}{\sum_{i = 1}^k\sum_{j = 1}^{n_i}(d_{ij} - D_i)^2} \]

上式中的分子部分可视作各组间变异，分母部分可视为组内变异，统计量 \(F\) 越大也即代表各组间差异较大，方差不等。也即在检验置信水平为 \(\alpha\) 时，当 \(F > F_{1-\alpha}(k-1, N-k)\) 时则拒绝原假设，认为各组间方差不相等，否则接受原假设。其中 \(F_{1-\alpha}(k-1, N-k)\) 是自由度分别为 \(k-1\) 与 \(N-k\) 的 F 分布界值。

案例#

例如我们有一份患者分别服用 A 药与 B 药 24 小时后的血压（blood pressure，BP）观察数据，如下表所示：

BP	组别

101.0	A
87.0	A
93.0	A
84.0	A
101.0	A
89.0	A
90.0	A
114.0	A
83.0	A
85.0	A
97.0	B
85.0	B
92.0	B
97.0	B
91.0	B
118.0	B
109.0	B
111.0	B
84.0	B
83.0	B

我们可以使用独立双样本 t 检验来比较服用两种药物后患者的血压值是否显著差异。在软件内操作步骤如下：

  1. 新建一个 “双样本 t 检验” 分析，并在 变量 和 组别 列内分别输入上述数据（图 438）。

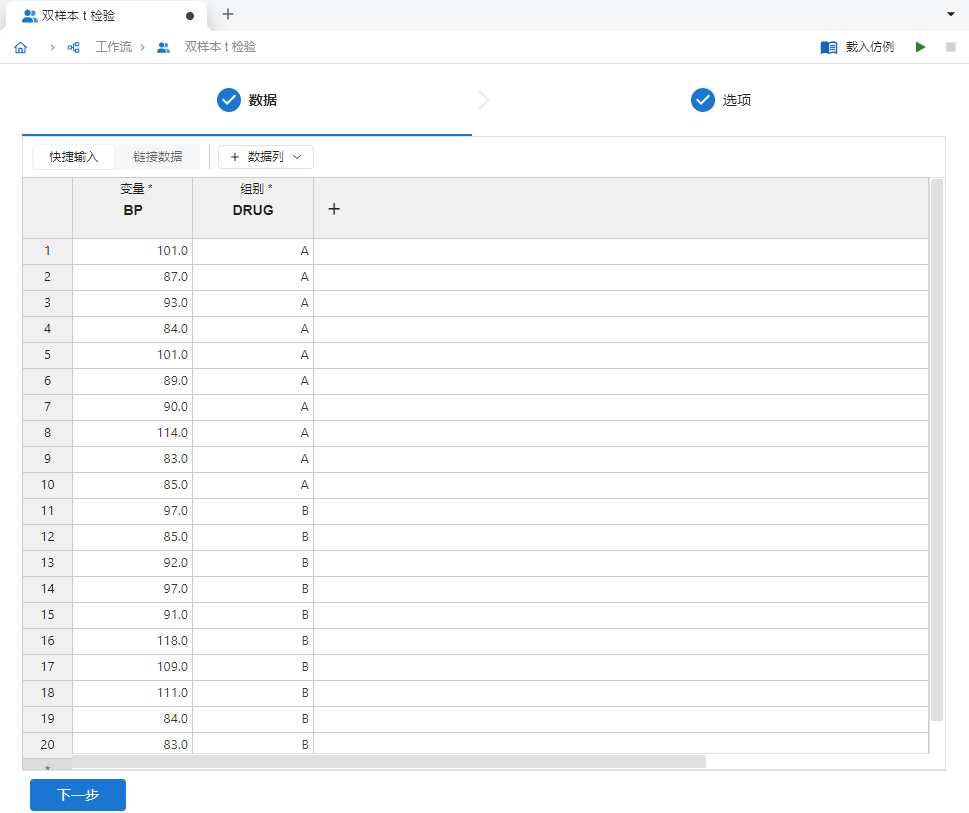
../../_images/stats-two-sample-t-example-data.png

图 438 输入数据示意图#

  1. 数据输入完成后，点击 “下一步” 按钮，在选项页面中确认组别定义分别为 A 与 B（图 439）。

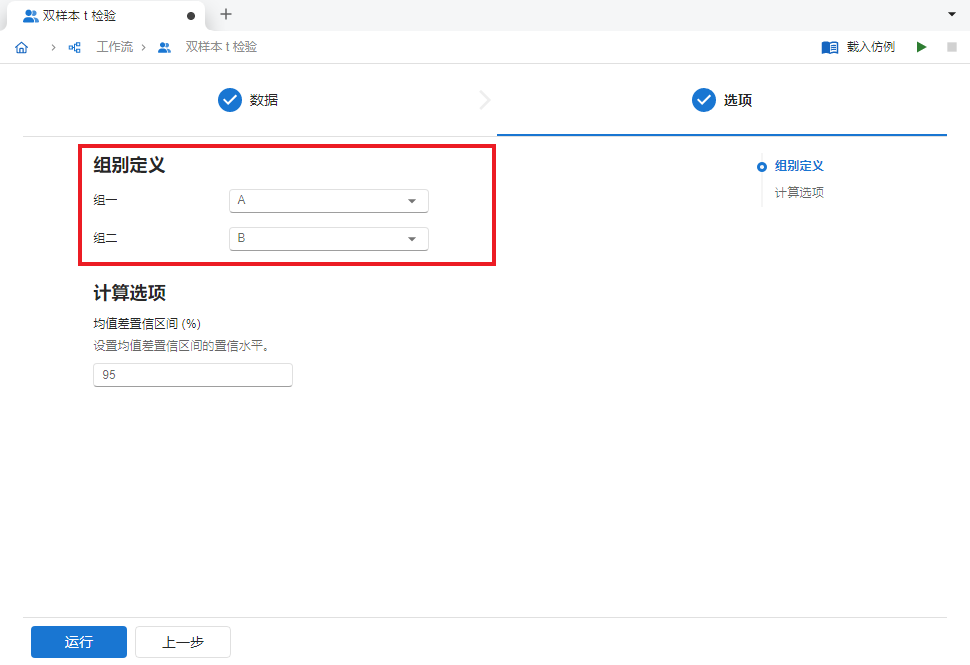
../../_images/stats-two-sample-t-example-options.png

图 439 组别定义选项示意图#

  1. 确认无误后点击 “运行” 按钮即可执行双样本 t 检验。在结果的 “独立双样本 t 检验” 表格中（图 440），我们首先检查 Levene's 检验结果，其 P 值为 0.47，可以认为两组数据等方差。随后检查假定等方差的双样本 t 检验结果，可以发现两组数据均值差为 -4，统计量 t 值为 -0.805，假设检验 P 值为 0.432。综上所述，可以认为服用两种药物后患者的血压值不存在差异。

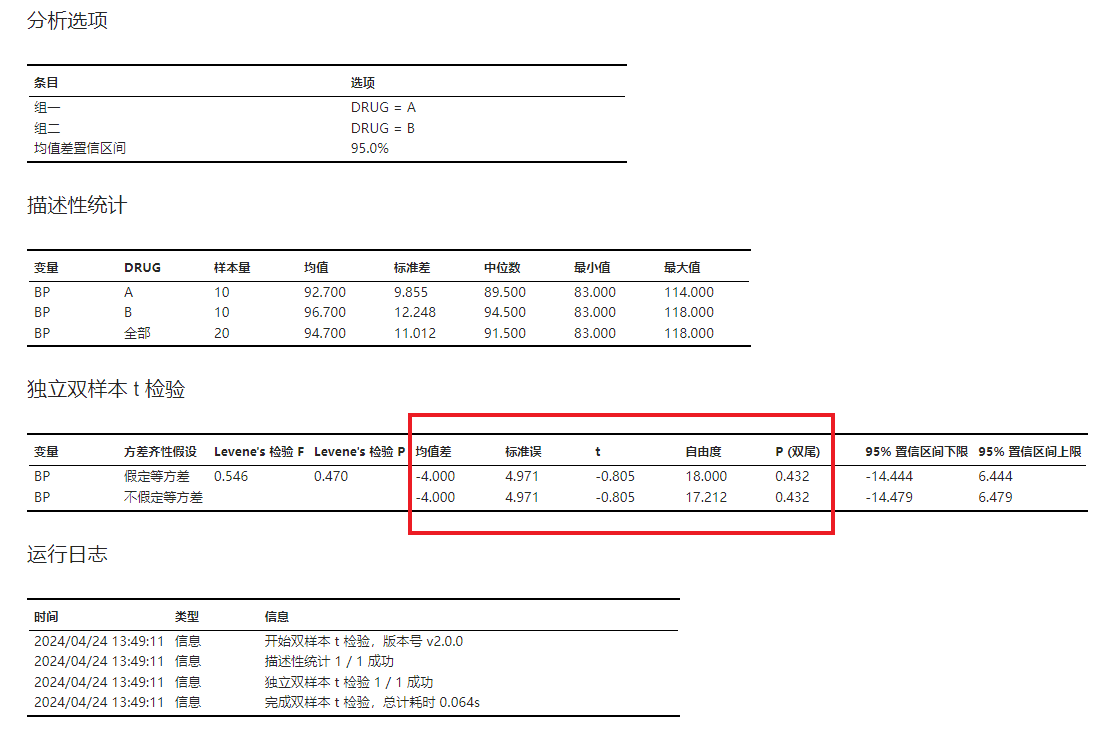
../../_images/stats-two-sample-t-example-result.png

图 440 检验结果示意图#