K-M 生存分析#

使用软件内的 “K-M 分析” 功能，可以对生存数据进行 Kaplan-Meier 生存分析并对多组间的生存率进行假设检验。

Kaplan-Meier 法目前是生存分析中最常用的方法之一。其为一种非参数方法，可以通过生存时间以及研究对象的状态数据来计算生存率并可对两组研究对象的生存情况进行比较分析。

本节中涉及的部分生存分析相关名词的含义可参见：生存分析常用概念。

数据映射关系#

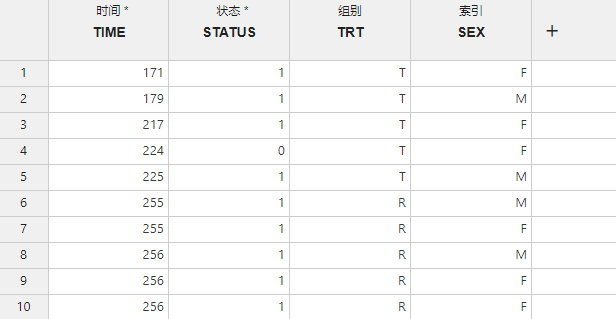
../../_images/stats-km-mapping.png

图 489 K-M 生存分析数据映射示意图#

  • 时间 （必选项，单选）：研究对象存活时间。

  • 状态 （必选项，单选）：研究对象的状态，指代是否发生事件或删失。

  • 组别 （可选项，单选）：研究对象所属的组别。不同组别间可对生存率进行组间比较。

  • 索引 （可选项，多选）：研究对象的索引。拥有不同索引值的对象将会被视作来自不同的来源并独立地进行生存率计算与组间比较。

分析选项#

数据选项#

../../_images/stats-km-option-data.png

图 490 数据选项示意图#

  • 事件定义：指定 “状态” 数据中代表事件发生的标识值。除此以外的标识值将均指代删失。可选项为 “状态” 数据中所有不重复的数据值。默认值为其中首个数据值。

计算选项#

../../_images/stats-km-option-calc.png

图 491 计算选项示意图#

  • 组间比较检验方法：选择组间比较的检验方法。可选项为 略过 与 Log Rank 检验（计算方法可见 Log Rank 检验 小节）。当有 “组别” 数据时，默认值为 Log Rank 检验；否则为 略过。

分析结果#

分析选项#

本次 K-M 生存分析的分析选项设置。示例可见 图 492。

../../_images/stats-km-result-options.png

图 492 分析选项表格示意图#

事件与删失#

各组内总样本数、事件发生数以及删失情况的汇总表格。示例可见 图 493。

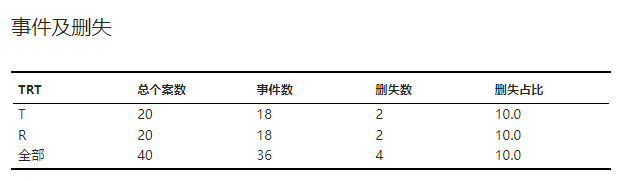
../../_images/stats-km-result-events.png

图 493 事件与删失表格示意图#

生存分析表#

各组在不同时间点累计生存率及其标准误的计算结果表格。示例可见 图 494。

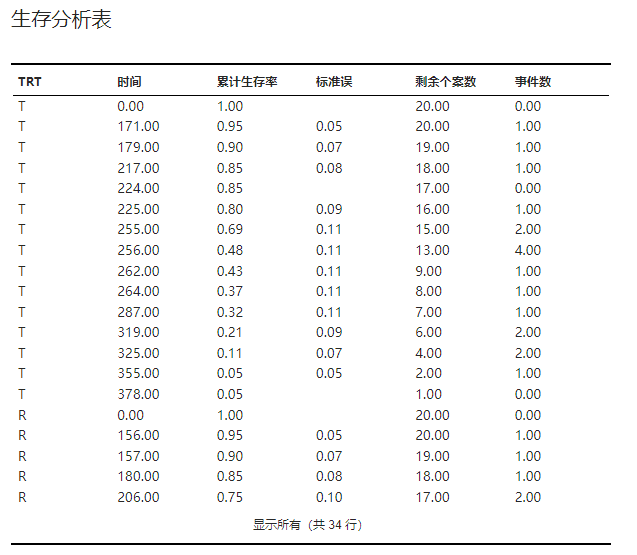
../../_images/stats-km-result-rate.png

图 494 生存分析表示意图#

中位生存时间#

各组中位生存时间（median survival time）、下四分位数（Q1）生存时间、上四分位数（Q3）生存时间及其置信区间的结果表格。示例可见 图 495。

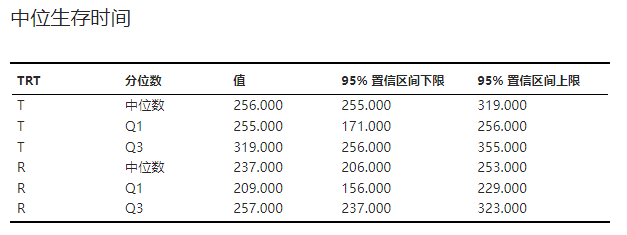
../../_images/stats-km-result-median.png

图 495 中位生存时间表格示意图#

Log Rank 组间比较#

Log Rank 组间比较结果，包含统计量 \(\chi^2\) 以及对应的 P 值。仅当在 计算选项 中选择了 Log Rank 检验 时才会出现此结果表格。示例可见 图 496。

../../_images/stats-km-result-log-rank.png

图 496 Log Rank 组间比较表格示意图#

生存曲线图#

各组数据的生存曲线图。以折线代表随时间变化的生存率，十字点代表删失，其不同的颜色指代不同的组别。示例可见 图 497。

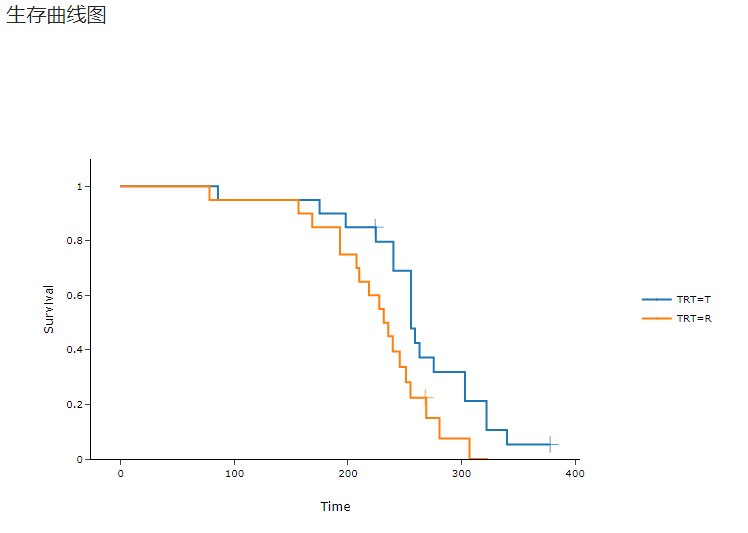
../../_images/stats-km-result-plot.png

图 497 生存曲线图示意图#

运行日志#

K-M 生存分析的运行日志，包含软件版本、运行时间、运行成功与否等信息。示例可见 图 498。

../../_images/stats-km-result-log.png

图 498 运行日志示意图#

统计理论#

估算生存率#

对于研究对象的生存函数，可以用统计学语言表述为：

\[ S(t) = Prob(T > t) \]

其中 \(T\) 为代表事件发生时间的随机变量，\(t\) 为观测时间。

Kaplan-Meier 法的基本思想是：只有当研究对象存活过时间 \(t_i\) 后，才有可能在 \(t_{i+1}\) 时刻发生事件。所以 \(t\) 时刻的生存率即是此前各时间点生存率的累乘。根据上述思想，Kaplan-Meier 法估算生存率的步骤如下：

  1. 将观测时间分为数个区间：\((0, u_1), (u_1, u_2), \cdots\) 区间的划分点一般为每一个事件或删失发生的时间点，也可以加入任意感兴趣的时间点。

  2. 对于每一个区间 \((u_{j-1}, u_j)\)，计算 \(p_j = S(j) / S(j-1)\)，其代表在存活时间超过 \(u_{j-1}\) 的研究对象中到 \(u_{j}\) 时刻依旧存活的对象的比例。

  3. 假设每一个区间内不同时发生事件与删失，此时 \(p_j\) 仅与 \(u_{j-1}\) 时刻后的可观测对象数量 \(n_j\) 以及区间内发生事件的对象数量 \(\delta_j\) 有关，可对 \(p_j\) 与 \(S(t)\)（设 \(u_k = t\)）做出如下估计：

\[\begin{split} \hat{p_j} = \frac{n_j - \delta_j}{n_j} \\ \hat{S}(t) = \prod_{j=1}^k \hat{p_j} \end{split}\]

例如对于以下样本量为 8 的数据：

事件发生时间

0.8，3.1，5.4，9.2

删失时间

1.0，2.7，7.0，12.1

区间划分情况、\(n_j\)、\(\delta_j\) 以及生存率估计值分别如下表所示：

区间划分点 \(u_j\)

观测数量 \(n_j\)

存活数量 \(n_j - \delta_j\)

生存率估计值 \(\hat{S}(u_j)\)

0.8

8

7

\(\frac{7}{8}\)

3.1

5

4

\(\frac{7}{8} \times \frac{4}{5}\)

5.4

4

3

\(\frac{7}{8} \times \frac{4}{5} \times \frac{3}{4}\)

9.2

2

1

\(\frac{7}{8} \times \frac{4}{5} \times \frac{3}{4} \times \frac{1}{2}\)

(12.1)

1

1

\(\frac{7}{8} \times \frac{4}{5} \times \frac{3}{4} \times \frac{1}{2} \times \frac{1}{1}\)

生存率估计值的样本方差由 Greenwood 公式给出（证明可见下方参考文献）：

\[ \hat{Var}(\hat{S}(t)) = (\hat{S}(t))^2 \sum_{j=1}^k (\frac{1}{n_j - \delta_j} - \frac{1}{n_j}) \]

参考文献

Kaplan, E. L. , & Meier, P. . (1958). Nonparametric estimation from incomplete observations. Journal of the American Statistical Association, 53, 457-481.

Greenwood, M. . (1926). "The natural duration of cancer," Reports on Public Health and Medical Subjects, No. 33. His Majesty's Stationery Office.

中位生存时间#

中位生存时间即生存率为 50% 时所对应的生存时间，可以反映生存时间的集中趋势，其表达式如下：

\[ \hat{t50} = min\{t_i | \hat{S}(t_i) ≤ 0.5\} \]

其中 \(t_i\) 为第 \(i\) 个个体的生存时间观测值，\(i = 1, 2, \cdots, N\)。

其置信水平为 \((1-\alpha) \times 100\%\) 的置信区间由所有满足下式的时间点 \(t_i\) 构成：

\[ \chi^2_{1-\frac{\alpha}{2}}(1) ≤ V_i ≤ \chi^2_{\frac{\alpha}{2}}(1) \]

其中，统计量 \(V_i\) 计算公式如下，其符合自由度为 1 的卡方分布：

\[ V_i = \frac{(\hat{S}(t_i)-0.5)^2}{\hat{Var}(\hat{S}(t_i))} \sim \chi^2(1) \]

参考文献

Crowley, B. J. . (1982). A confidence interval for the median survival time. Biometrics, 38(1), 29-41.

例如，现有以下数据：

事件发生时间

10，15，23，30，35，52

删失时间

100

可以按下表计算中位生存时间及其 95% 置信区间：

观测时间 \(t_i\)

生存率 \(\hat{S}(t_i)\)

样本方差 \(\hat{Var}(\hat{S}(t_i))\)

统计量 \(V_i\)

\(\chi^2_{1-0.025}(1)\)

\(\chi^2_{0.025}(1)\)

10

0.857

0.017

7.292

0.001

5.024

15

0.714

0.029

1.575

0.001

5.024

23

0.571

0.035

0.146

0.001

5.024

30

0.429

0.035

0.146

0.001

5.024

35

0.286

0.029

1.575

0.001

5.024

52

0.143

0.017

7.292

0.001

5.024

由上表可知，中位生存时间为 30，其 95% 置信区间为 [10, 52]。

Log Rank 检验#

Log Rank 检验为比较生存函数时最常用的假设检验方法。Log Rank 检验属于非参数检验，其基本思想时：若两组对象来自同一个总体，则它们在不同时间的实际事件发生数与理论事件发生数应当相差不大。

所以，Log Rank 检验的原假设为：两总体生存函数相同 \(S_1(t)=S_2(t)\)；备择假设为：\(S_1(t) \neq S_2(t)\)。

对于两组对象中不重合的发生事件的时间 \(1, 2, \cdots, J\)，现定义以下量：

\[ \begin{align}\begin{aligned} &\ N_j = N_{1, j} + N_{2, j}\\&\ O_j = O_{1, j} + O_{2, j} \end{aligned}\end{align} \]

其中 \(j = 1, 2, \cdots, J\)；\(N_{1, j}\) 与 \(N_{2, j}\) 分别为两组对象在 \(j\) 时刻处于风险（未发生事件也未删失）的对象数；\(O_{1, j}\) 与 \(O_{2, j}\) 为在 \(j\) 时刻发生事件的对象数。

可知 \(O_{i, j}\) （\(i\) 为 1 或 2）服从以下超几何分布（hypergeometric distribution）：

\[ O_{i, j} \sim h(N_j, N_{i, j}, O_j) \]

因此其期望与方差分别为：

\[ E_{i,j} = E(O_{i, j}) = N_{i, j} \frac{O_j}{N_j} \]
\[ V_{i,j} = Var(O_{i, j}) = E_{i,j} (\frac{N_j - O_j}{N_j}) (\frac{N_j - N_{i, j}}{N_j - 1}) \]

由此我们可以构建以下统计量：

\[ Z = \frac{\sum_{j=1}^J (O_{i, j} - E_{i, j})}{\sqrt{\sum_{j=1}^J V_{i,j}}} \sim N(0, 1) \]

设假设检验显著性水平为 \(\alpha\)，当 \(|Z| > Z_{1 - \frac{\alpha}{2}}\) 时则拒绝原假设，认为两组对象的生存曲线不一致，否则接受原假设。

当推广至多个总体时，原假设为 \(S_1(t)=S_2(t)=\cdots=S_I(t)\)；备择假设为 \(S_1(t), S_2(t), \cdots, S_I(t)\) 不全相等。

此时的统计量为：

\[ \chi^2 = \sum_{i=1}^I \frac{[\sum_{j=1}^J (O_{i, j} - E_{i, j})]^2}{\sum_{j=1}^J V_{i,j}} \sim \chi^2(I-1) \]

其中 \(i = 1, 2, \cdots, I\)。

参考文献

Peto, R. , & Peto, J. . (1972). Asymptotically efficient rank invariant test procedures. Journal of the Royal Statistical Society Series A (General), 135(2).

Prentice, R. L., & Marek, P. (1979). A qualitative discrepancy between censored data rank tests. Biometrics, 35(4), 861–867.

案例#

我们现有某中心对晚期肺癌患者的随访数据，欲比较不同性别患者的生存率是否有差异：

数据如下，其中 TIME 列为生存事件（天）；STATUS 列为患者状态（1 为删失、2 为死亡）；SEX 列为患者性别。

TIME	STATUS  SEX

116	2	Male
144	2	Male
163	2	Male
176	2	Male
180	2	Male
181	2	Male
188	1	Male
218	2	Male
225	1	Male
246	2	Male
267	2	Male
284	1	Male
303	2	Male
303	1	Male
457	2	Male
524	2	Male
558	2	Male
883	2	Male
61	2	Female
62	2	Female
122	2	Female
145	2	Female
252	1	Female
276	1	Female
345	2	Female
376	1	Female
559	1	Female
588	1	Female
705	2	Female
730	2	Female

  1. 新建一个 “K-M 生存分析”，在 时间、状态 与 组别 内分别输入上述数据，如 图 499 所示：

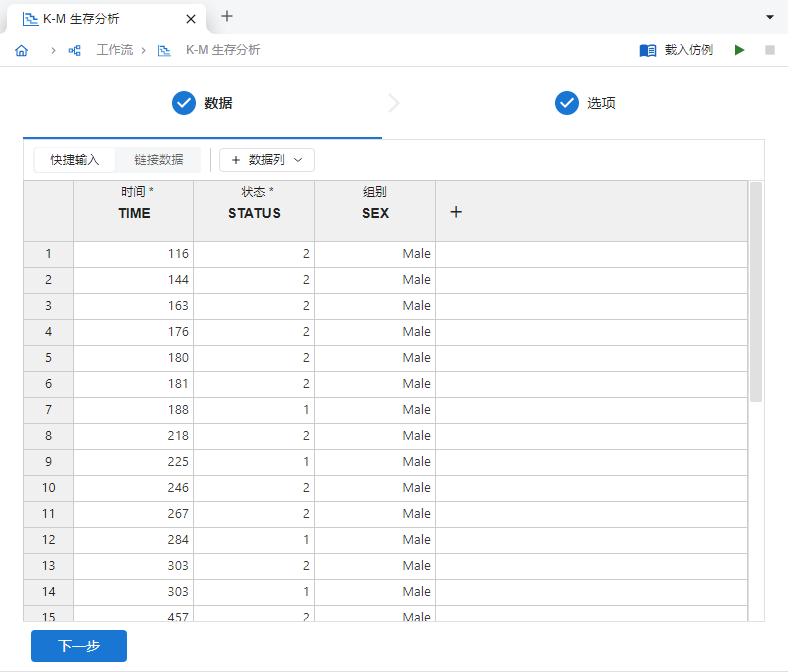
../../_images/stats-km-example-data.png

图 499 输入数据示意图#

  1. 输入完成后，点击 “下一步” 按钮，在 “事件定义” 选项中选择 2；在 “组间比较检验方法” 中选择 Log Rank 检验（图 500）。

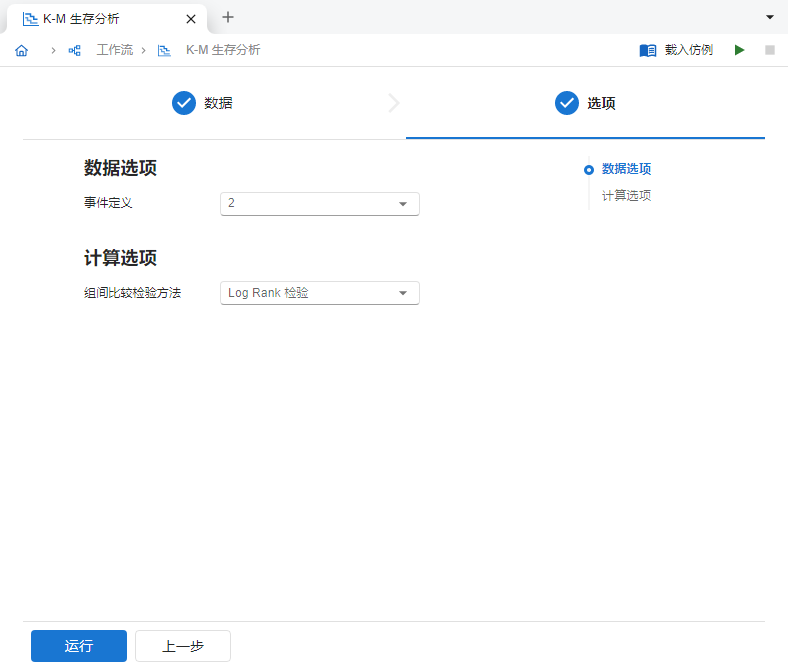
../../_images/stats-km-example-option.png

图 500 选项设置示意图#

  1. 设置完成后，点击 “运行” 按钮以执行生存分析。在结果的 “Log Rank 检验” 表格内可以发现检验统计量 \(\chi^2\) 为 0.847，P 值为 0.357。因此我们可以认为不同性别晚期肺癌患者的生存率没有显著差异。我们也可以进一步通过生存曲线图获知生存率的变化趋势（图 501）。

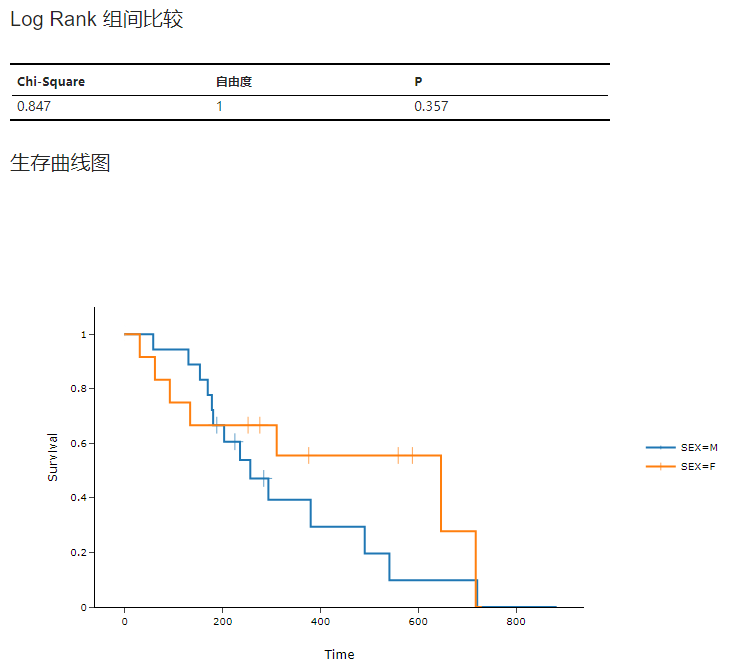
../../_images/stats-km-example-result.png

图 501 检验结果以及生存曲线图示意图#