相关性分析#

使用软件内的 “相关性分析” 功能，我们可以计算两个变量间的相关系数（correlation coefficient）并检验其显著性。

数据映射关系#

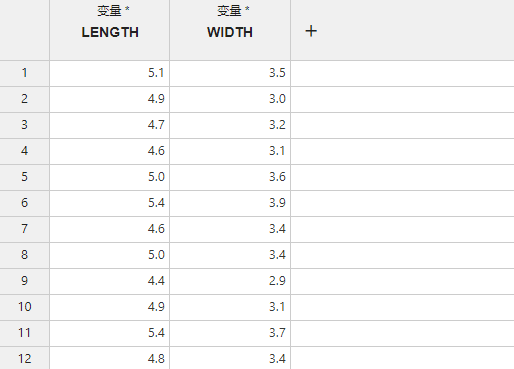
../../_images/stats-corr-mapping.png

图 517 相关性分析数据映射示意图#

  • 变量 （必选项，多选）：变量数据。将与另一个变量数据分析两者间的相关性。

备注

至少需要两个变量才能进行相关性分析。如果存在多个变量则将两两进行相关性分析。

分析选项#

计算选项#

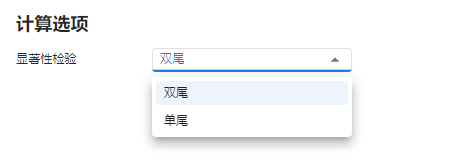
../../_images/stats-corr-option-calc.png

图 518 计算选项示意图#

  • 显著性检验：选择相关系数假设检验中计算双尾 P 值抑或是单尾 P 值（右尾）。可选项为 双尾 或 单尾。统计量相关计算方法可参见 相关系数的假设检验 小节。默认值为 双尾。

分析结果#

分析选项#

本次相关性分析的分析选项设置。示例可见 图 519。

../../_images/stats-corr-result-options.png

图 519 分析选项表格示意图#

描述性统计#

各变量的描述性统计结果，包括均值、标准差、中位数等。示例可见 图 520。

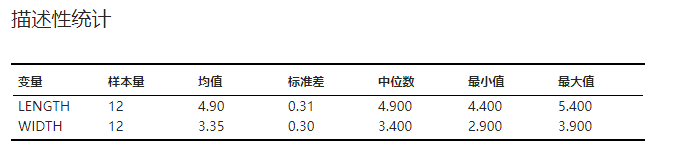
../../_images/stats-corr-result-des-results.png

图 520 描述性统计表格示意图#

双变量相关性#

变量间相关性分析结果，包括 Pearson/Spearman 相关系数以及对应的假设检验结果。统计量的计算方法可参见 相关系数 小节。示例可见 图 521。

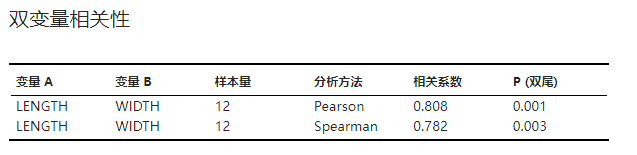
../../_images/stats-corr-result-corr-test.png

图 521 双变量相关性表格示意图#

运行日志#

相关性分析的运行日志，包含软件版本、运行时间、运行成功与否等信息。示例可见 图 522。

../../_images/stats-corr-result-log.png

图 522 运行日志示意图#

统计理论#

协方差#

设 \((X, Y)\) 是一个二维随机变量，若 \(E[(X-E(X))(Y-E(Y))]\) 存在，则此数学期望称作 \(X\) 与 \(Y\) 的协方差（covariance）。记作：

\[ Cov(X, Y) = E[(X-E(X))(Y-E(Y))] \]

协方差的大小可以描述两个变量的相关性关系。当 \(Cov(X, Y) > 0\) 时，称作 \(X\) 与 \(Y\) 正相关，此时 \(X\) 与 \(Y\) 应当同时增加或减小；反之则称为 \(X\) 与 \(Y\) 负相关；当 \(Cov(X, Y) = 0\) 时，则 \(X\) 与 \(Y\) 不相关。

相关系数#

由于协方差的大小和数据量纲有关，所以可以对其进行标准化以消除量纲的影响：

\[ Corr(X,Y) = \frac{Cov(X, Y)}{\sqrt{Var(X)} \sqrt{Var(Y)}} \]

\(Corr(X,Y)\) 即被称为 \(X\) 与 \(Y\) 的相关系数。相关系数与协方差同符号，取值范围为 \(-1 ≤ Corr(X, Y) ≤ 1\)，其大小同样可以反映 \(X\) 与 \(Y\) 正相关、负相关或不相关。

根据上述定义，来源于总体的两个连续样本 \(x\) 与 \(y\) 的相关系数计算公式为：

\[ r = \frac{\sum_{i=1}^n (y_i - \bar y)(x_i - \bar x)}{\sqrt{\sum_{i=1}^n (x_i - \bar x)^2} \sqrt{\sum_{i=1}^n (y_i - \bar y)^2}} \]

这里 \(r\) 被称为 Pearson 相关系数。

对于离散样本，则可以将 \(x\) 与 \(y\) 放在一起并从小到大排列得到每个个体的秩 \(x_{(i)}\) 与 \(y_{(i)}\)（秩的概念可以参考 非参检验）。将 \(x_{(i)}\)、\(y_{(i)}\) 以及各自的平均秩带入上述相关系数计算公式，得到的结果则称为 Spearman 相关系数。

相关系数的假设检验#

相关系数假设检验的原假设为：两个变量之间无相关性，即 \(r=0\)；备择假设为两个变量间存在相关性，即 \(r \neq 0\)。

根据上述对假设的描述，我们容易想到此时可以使用 t 检验来完成假设检验，因此构造如下统计量：

\[ t_r = \frac{r - 0}{\sqrt{\frac{1 - r^2}{n - 2}}} \]

统计量 \(t_r\) 服从自由度为 \(n-2\) 的 t 分布，证明可见下方参考文献。

当假设检验显著性水平为 \(\alpha\) 时，若 \(|t| > t_{1-\frac{\alpha}{2}, n-2}\) 时则拒绝原假设，认为两变量间存在相关性，否则接受原假设。

参考文献

N. A. Rahman. (1968). A Course In Theoretical Statistics. Charles Griffin and Co. Ltd. .

案例#

我们现有一组受试者 BMI 与低密度脂蛋白（low density lipoprotein，LDL）的数据（如下表），我们欲研究 BMI 与 LDL 间是否有相关性以判断肥胖是否为动脉粥样硬化的危险因素之一。使用相关性分析功能我们可以达成以上分析目的。

BMI     LDL

19.2	75.0
20.3	81.2
21.1	87.8
21.7	79.2
24.3	98.6
24.4	91.4
24.7	88.2
25.2	72.0
25.8	90.1
26.0	120.4
29.7	103.4
30.5	110.6
31.9	99.6
32.0	130.0
34.5	150.6
38.0	147.2

  1. 新建一个 “相关性分析”，在两个 变量 列内分别输入上述数据，如 图 523 所示：

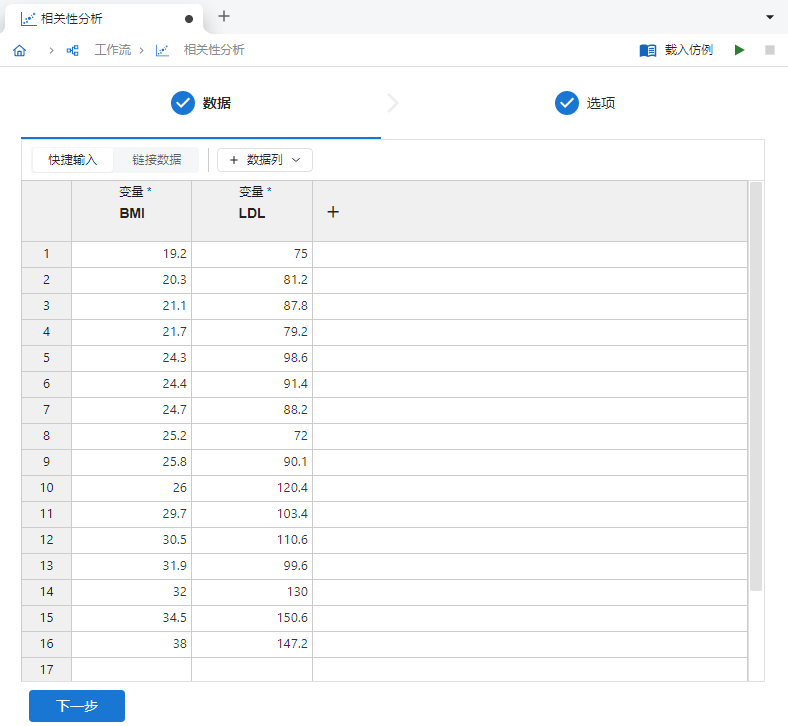
../../_images/stats-corr-example-data.png

图 523 输入数据示意图#

  1. 输入完成后，点击 “下一步” 按钮，确认选择计算 双尾 P 值 （图 524）。

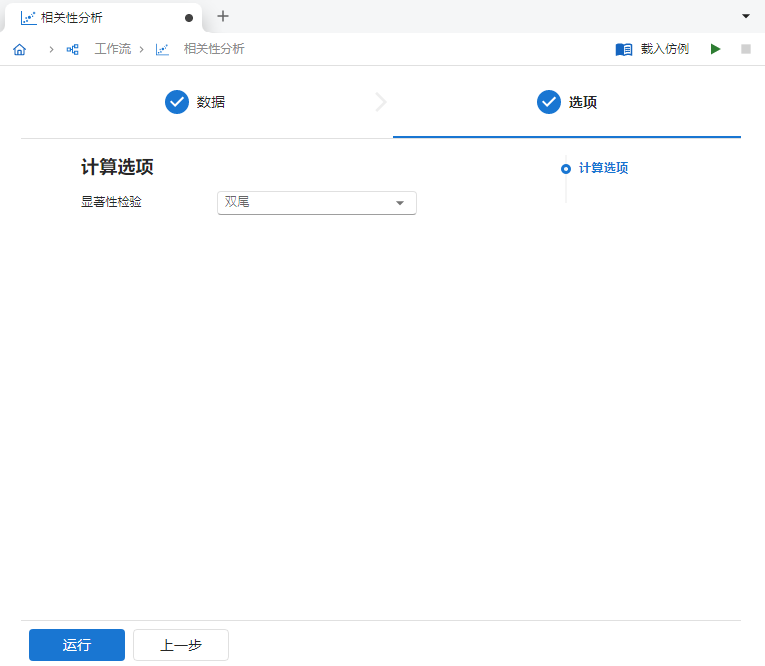
../../_images/stats-corr-example-option.png

图 524 计算选项设置示意图#

  1. 设置完成后，点击 “运行” 按钮以执行相关性分析。在结果中我们查看 “双变量相关性” 表格，由于 BMI 为连续变量，我们关注 Pearson 相关系数——其值为 0.860，对应的 P 值为 0.000（图 525）。根据此结果我们可以认为 BMI 与 LDL 之间正相关，肥胖可能是动脉粥样硬化的危险因素之一。

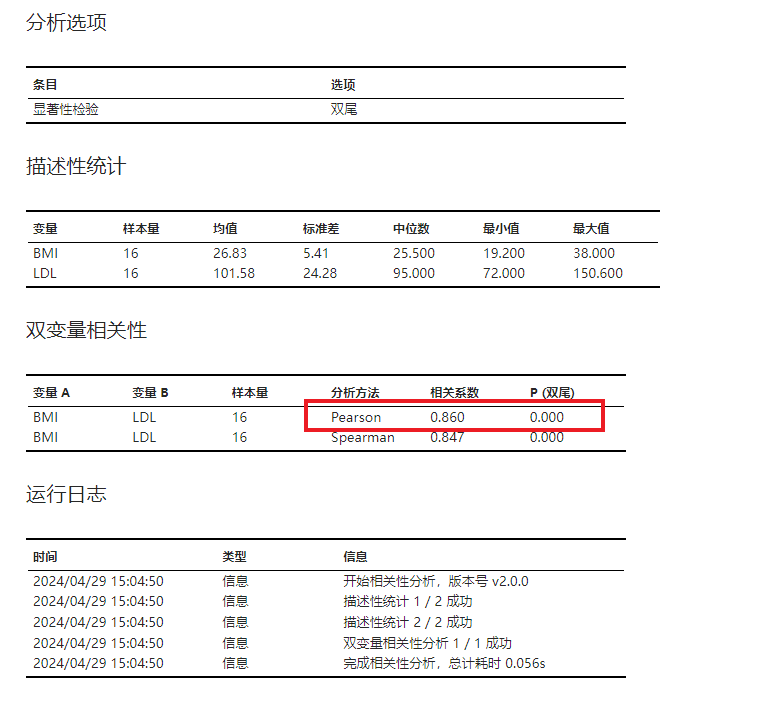
../../_images/stats-corr-example-result.png

图 525 相关性分析结果示意图#