非参检验#

通过软件内的 “非参检验” 功能，可以执行独立双样本的非参检验（nonparametric test）。

非参检验在统计检验过程中不对总体分布做任何假设，也不涉及任何有关总体分布的参数，因此常用于非正态数据间的比较。

数据映射关系#

../../_images/stats-nonparametric-mapping.png

图 451 非参检验数据映射示意图#

  • 变量 （必选项，多选）：需要检验的变量数据。若有多个变量，则将分别进行检验。

  • 组别 （必选项，单选）：组别数据。用于区分变量数据所属的组别，拥有相同组别值的变量数据将被视作同一组。

分析选项#

组别定义#

../../_images/stats-nonparametric-option-group.png

图 452 组别定义选项示意图#

  • 组一：定义第一组数据的组别值。默认值为组别数据中出现的第一个不重复的字符串。

  • 组二：定义第二组数据的组别值。默认值为组别数据中出现的第二个不重复的字符串。

计算选项#

../../_images/stats-nonparametric-option-calc.png

图 453 计算选项示意图#

  • 检验方法：非参检验的方法。可选项为 Mann-Whitney U 检验，相关计算方法可参见 统计理论 小节。默认值为 Mann-Whitney U 检验。

分析结果#

分析选项#

本次非参检验的分析选项设置。示例可见 图 454。

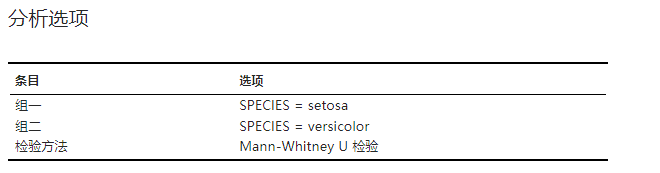
../../_images/stats-nonparametric-result-options.png

图 454 分析选项表格示意图#

描述性统计#

各组数据以及全部数据的描述性统计结果，包括均值、标准差、中位数等。示例可见 图 455。

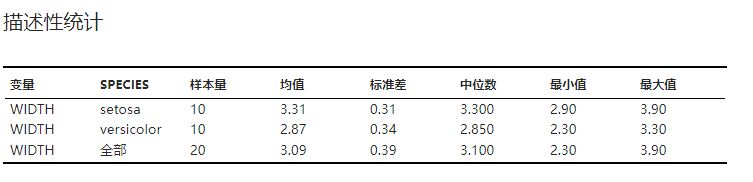
../../_images/stats-nonparametric-result-des-results.png

图 455 描述性统计表格示意图#

秩摘要#

各组数据秩（rank）的计算结果，包括平均秩（mean rand）与秩和（sum of ranks）。秩的概念以及秩和的计算方法可参见 秩的概念 小节。示例可见 图 456。

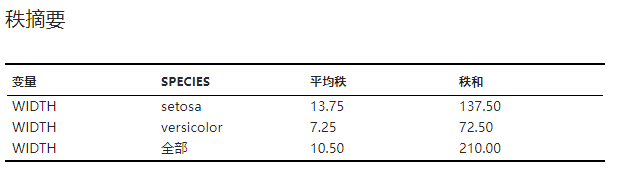
../../_images/stats-nonparametric-result-ranks.png

图 456 秩摘要表格示意图#

独立双样本 Mann-Whitney U 检验#

Mann-Whitney U 检验的结果，包括统计量 U、近似 P 值以及精确 P 值（相关定义可参见 计算拒绝域 小节）。示例可见 图 457。

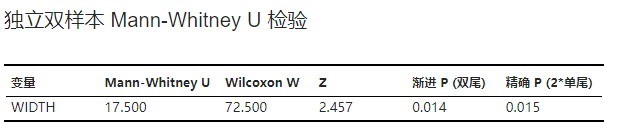
../../_images/stats-nonparametric-result-test-results.png

图 457 独立双样本 Mann-Whitney U 检验表格示意图#

运行日志#

非参检验的运行日志，包含软件版本、运行时间、运行成功与否等信息。示例可见 图 458。

../../_images/stats-nonparametric-result-log.png

图 458 运行日志示意图#

统计理论#

Mann-Whitney U 检验的统计假设#

现有两组样本分别来自两个除均值外均相同的总体，两个总体的均值记作 \(\mu_1\) 与 \(\mu_2\)。

则 Mann-Whitney U 检验的原假设为：\(\mu_1 = \mu_2\)；备择假设为 \(\mu_1 \neq \mu_2\)。

秩的概念#

设 \(X\) 为一个总体，将一样本量为 \(n\) 的样本观测值自小到大排序并编号得到：

\[ x_{(1)} < x_{(2)} < \cdots < x_{(n)} \]

此时，\(x_{(i)}\) 的下标 \(i\) 即为 \(x_{(i)}\) 的秩（rank）。

现再从两个总体 \(X_1\) 与 \(X_2\) 中分别取出样本量为 \(n_1\) 与 \(n_2\) 的样本观测值。把这 \(n_1 + n_2\) 个样本放在一起并从小到大排列并得到每个样本的秩。随后将原本属于 \(X_1\) 的样本的秩相加，记作 \(R_1\)，称作 \(X_1\) 的秩和。同样的，\(X_2\) 的秩和记作 \(R_2\)。

显然，\(R_1\) 与 \(R_2\) 满足：\(R_1 + R_2 = \frac{(1 + n_1 + n_2)(n_1 + n_2)}{2}\)。

计算统计量#

Mann-Whitney U 检验计算的统计量为 \(U\)，其为 \(U_1\) 与 \(U_2\) 中的较小值，它们的计算公式如下：

\[ \begin{align}\begin{aligned}\begin{split} U_1 = n_1 n_2 + \frac{n_1(n_1 + 1)}{2} - R_1 \\\end{split}\\U_2 = n_1 n_2 + \frac{n_2(n_2 + 1)}{2} - R_2 \end{aligned}\end{align} \]

参考文献

Mann, H. B. , & Whitney, D. R. . (1947). On a test of whether one of two random variables is stochastically larger than the other. Annals of Mathematical Statistics, 18(1), 50-60.

计算拒绝域#

近似算法#

当样本量大于等于 8 时，秩和 \(R\) 的分布近似于正态分布，以 \(R_1\) 为例：

\[ \begin{align}\begin{aligned}\begin{split} \mu_{R_1} = E(R_1) = \frac{n_1(n_1 + n_2 + 1)}{2} \\\end{split}\\\sigma_{R_1}^2 = D(R_1) = \frac{n_1 n_2(n_1 + n_2 + 1)}{12} \end{aligned}\end{align} \]
\[ R_1 \sim N(\mu_{R_1}, \sigma_{R_1}^2) \]

因此对于秩和的实测值 \(r_1\) 可以计算统计量：

\[ z = \frac{r_1 - \mu_{R_1}}{\sigma_{R_1}} \]

当显著性水平为 \(\alpha\) 时，若 \(|z| ≥ z_{1-\frac{\alpha}{2}}\) 则拒绝原假设，认为两个总体均值不等，否则接受原假设。

精确算法#

对于计算的统计量 \(U\)，其精确 P 值计算方法为：

\[ p_{n_1 n_2}(U) = \frac{n_1}{n_1 + n_2} p_{{n_1}-1 n_2}(U - n_2) + \frac{n_2}{n_1 + n_2} p_{{n_1 n_2}-1}(U) \]

当显著性水平为 \(\alpha\) 时，若 \(p_{n_1 n_2}(U) ≤ \alpha\) 则拒绝原假设，认为两个总体均值不等，否则接受原假设。

案例#

我们现有一份患者服用 A 药与 B 药后血糖的观测数据（如下表所示），我们欲比较两组间血糖均值是否有显著差异。

血糖	组别
87	A
69	A
85	A
89	A
80	A
68	A
82	A
92	A
94	A
88	A
83	B
77	B
81	B
88	B
73	B
81	B
98	B
91	B
87	B
78	B

  1. 首先我们通过 直方图 可以发现，两组样本数据的分布基本呈偏态（图 459），提示我们应当使用非参检验。

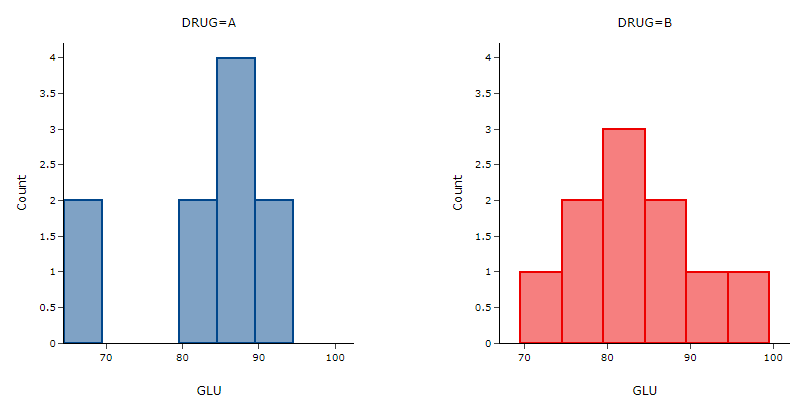
../../_images/stats-nonparametric-example-histogram.png

图 459 案例数据直方图示意图#

  1. 随后我们新建一个 “非参检验” 分析，并在 变量 和 组别 列内分别输入上述数据（图 460）。

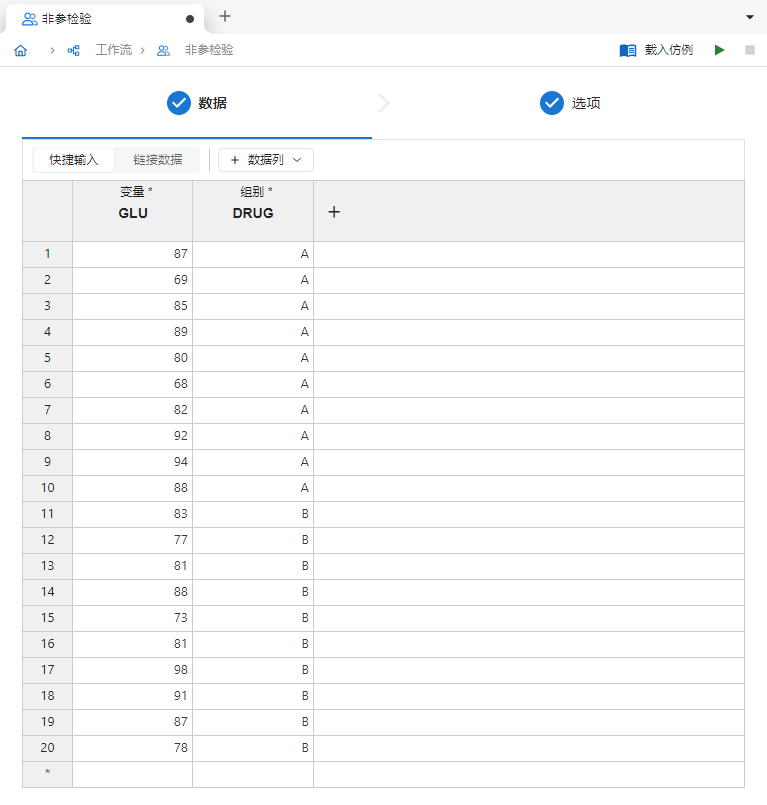
../../_images/stats-nonparametric-example-data.png

图 460 输入数据示意图#

  1. 数据输入完成后，点击 “下一步” 按钮，在选项页面中确认检验方法与组别定义无误（图 461）。

../../_images/stats-nonparametric-example-options.png

图 461 分析选项设置示意图#

  1. 设置完成后，点击 “运行” 按钮以执行非参检验。在结果的 “独立双样本 Mann-Whitney U 检验” 表格中（图 462），我们可以得知统计量 U 值为 46，假设检验 P 值为 0.762 与 0.791。根据此结果我们可以认为服用两种药物后患者的血糖值不存在差异。

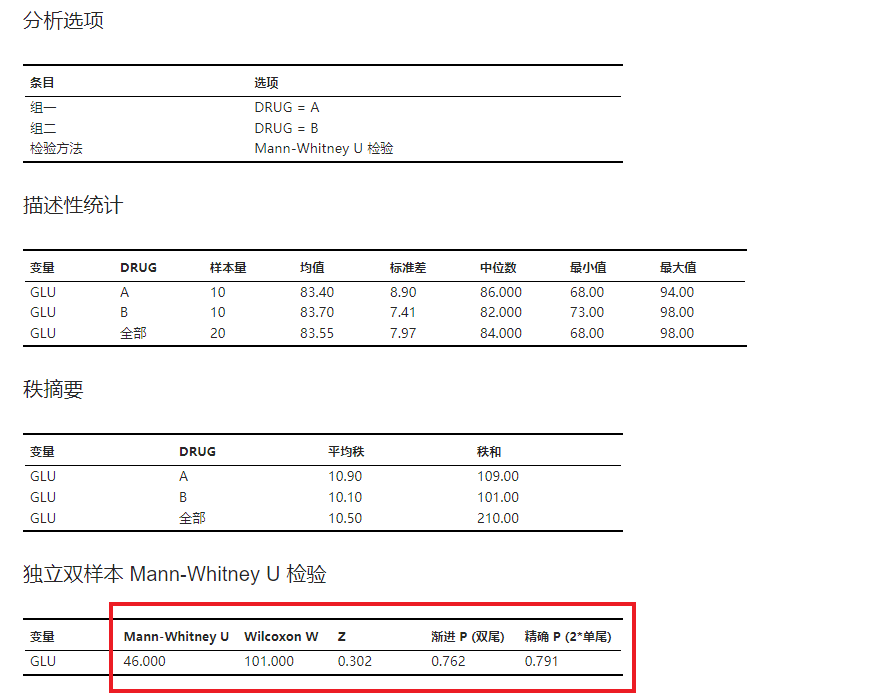
../../_images/stats-nonparametric-example-result.png

图 462 非参检验分析结果示意图#