2.4. 方差分析

通过软件内的 “方差分析” 功能，可以对数据进行单因素方差分析（one-way ANOVA）。

单因素方差分析一般用于检验互相独立且符合正态分布的各组数据间的均值是否相等，且可以进行组间均值的两两比较（pairwise comparison）。

2.4.1. 数据映射关系

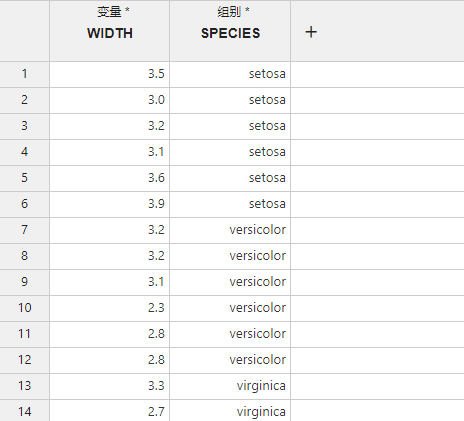
图 2.127 方差分析数据映射示意图

• 变量 （必选项，多选）：需要检验的变量数据。若有多个变量，则将分别进行检验。

• 组别 （必选项，单选）：组别数据。用于区分变量数据所属的组别，拥有相同组别值的变量数据将被视作同一组。

2.4.2. 分析选项

事后比较

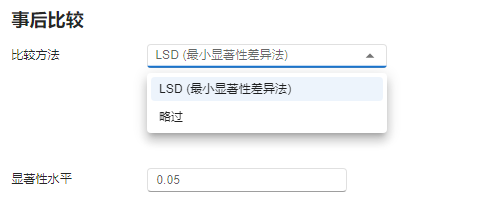
图 2.128 事后比较选项示意图

• 比较方法：选择事后两两比较（pairwise comparison）的方法。可选项为 LSD (最小显著性差异法) 与 略过。若选择 略过 则不进行事后比较。默认值为 LSD (最小显著性差异法)。LSD 方法相关内容可参见 LSD 事后比较 小节。

• 显著性水平：LSD 检验的显著性水平。将影响计算的均值差置信区间大小（例如输入 0.05 时将计算均值差的 95% 置信区间），相关计算公式可详见 计算均值差置信区间。默认值为 0.05。

2.4.3. 分析结果

分析选项

本次方差分析的分析选项设置。示例可见 图 2.129。

图 2.129 分析选项表格示意图

描述性统计

各组数据以及全部数据的描述性统计结果，包括均值、标准差、中位数等。示例可见 图 2.130。

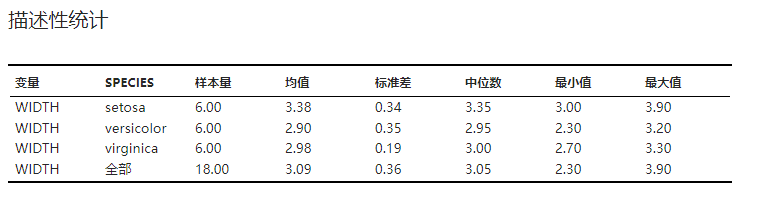
图 2.130 描述性统计表格示意图

单因素方差分析

单因素方差分析的结果，包括组间与组内的均方（mean square）、统计量 F 值及对应的 P 值，其详细计算方法可参考 统计理论 小节。示例可见 图 2.131。

图 2.131 单因素方差分析表格示意图

LSD 事后比较

LSD 事后比较的结果，包括各组两两间的均值差、检验 P 值与均值差置信区间。仅当在 事后比较 选项内选择 LSD (最小显著性差异法) 才会出现此表格。示例可见 图 2.132。

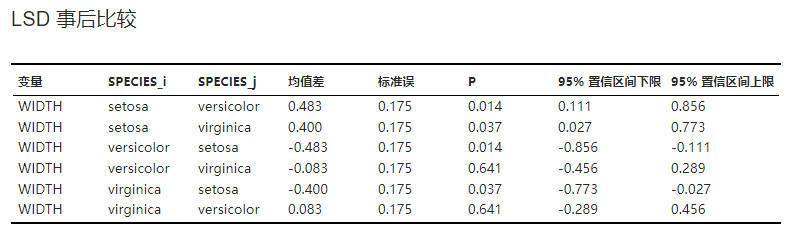
图 2.132 LSD 事后比较表格示意图

运行日志

方差分析的运行日志，包含软件版本、运行时间、运行成功与否等信息。示例可见 图 2.133。

图 2.133 运行日志示意图

2.4.4. 统计理论

方差分析的统计假设

某因素 \(A\) 有 \(k\) 个水平，各水平的样本分别记作 \(X_1, X_2, \cdots, X_k\)。假设各个样本分别来自均值为 \(\mu_1, \mu_2, \cdots, \mu_k\) 、标准差为 \(\sigma\) 的正态总体。

此时单因素方差分析的原假设为：\(\mu_1 = \mu_2 = \cdots = \mu_k\)；

备择假设为：\(\mu_1, \mu_2, \cdots, \mu_k\) 不全相等。

我们引入 \(\delta_i\) 来进一步表示水平 \(A_i\) 下组内样本均值（假设样本量为 \(n_i\)）与整体均值（假设样本量为 \(N\)）的差异，计算公式如下：

\[ \delta_i = \mu_i - \frac{1}{N} \sum_{i=1}^{k}{n_i \mu_i} \]

当且仅当 \(\mu_1 = \mu_2 = \cdots = \mu_k\) 时，\(\delta_1 = \delta_2 = \cdots = \delta_k = 0\)。

所以原假设可以修改为：\(\delta_1, \delta_2, \cdots, \delta_k\) 全部为零；备择假设为 \(\delta_1,\delta_2, \cdots, \delta_k\) 不全为零。

计算均方

为了计算与上述假设相关的统计量，我们首先引入总偏差平方和 \(S_T\)。其可以反映数据整体的差异情况，公式如下：

\[ \begin{align}\begin{aligned}\begin{split} \bar {X_i} = \frac{1}{n_i} \sum_{j = 1}^{n_i} X_{ij} \\\end{split}\\\bar X = \frac{1}{k} \sum_{i = 1}^{k} \bar {X_i} \end{aligned}\end{align} \]

\[\begin{split} S_T & = \sum_{i=1}^{k} \sum_{j=1}^{n_i} (X_{ij} - \bar X)^2 \\ & = \sum_{i=1}^{k} \sum_{j=1}^{n_i} [(X_{ij} - \bar {X_i}) + (\bar {X_i} - \bar X)]^2 \\ & = \sum_{i=1}^{k} \sum_{j=1}^{n_i} (X_{ij} - \bar {X_i})^2 + \sum_{i=1}^{k} \sum_{j=1}^{n_i} (\bar {X_i} - \bar {X})^2 & = S_E + S_A \end{split}\]

根据卡方分布的定义，可知：

\[\begin{split} \frac{S_E}{\sigma^2} \sim \chi^2(N - k) \\ E(S_E) = (N - k) \sigma^2 \end{split}\]

对于 \(S_A\)，其期望为：

\[\begin{split} E(S_A) &= E[\sum_{i=1}^k {n_i {\bar{X_i}}^2} - N {\bar X}^2] \\ & = \sum_{i=1}^k {n_i [\frac{\sigma^2}{n_i} + (\mu + \delta_i)^2]} - N(\frac{\sigma^2}{N} + \mu^2) \\ & = (k - 1)\sigma^2 + \sum_{i=1}^{k}{n_i \delta_i^2} \end{split}\]

对于 \(S_A\) 而言，当原假设成立时有：\(\frac{S_A}{\sigma^2} \sim \chi^2(k-1)\)。

一般而言，我们称 \(S_A\) 为组间平方和、\(S_E\) 为组内平方和，两者分别代表组间与组内的变异大小；称 \(\frac{S_A}{k-1}\) 与 \(\frac{S_E}{n-k}\) 为均方。

构建统计量

此时我们可以构建似然比检验统计量 F：

\[ F = \frac{S_A (k-1)}{S_E (N-k)} \]

由于 \(E(S_E (N-k))\) 恒等于 \(\sigma^2\)，而 \(E(S_A (k-1)) = \sigma^2 + \frac{1}{k-1} \sum_{i=1}^k{n_i \delta_i^2}\)。当且仅当原假设成立时，\(F \sim F(k-1, N-k)\)。若原假设不成立，则 \(F\) 有偏大的趋势（因为此时 \(E(S_A (k-1)) > \sigma^2\)），所以原假设的拒绝域为 \(F ≥ F_{1 - \alpha}(k-1, N-k)\)。

计算均值差置信区间

已知因素 \(A\) 的水平 \(a\) 与水平 \(b\) 的组内均值分别为 \(\bar{X_a}\)、\(\bar{X_b}\)。

易知：\(\bar{X_a} \sim N(\mu_a, \sigma^2/{n_a})\)、\(\bar{X_b} \sim N(\mu_b, \sigma^2/{n_b})\)。且有：\(E(\bar{X_a}) = \mu_a\)、\(E(\bar{X_b}) = \mu_b\)、\(E(\bar{X_a} - \bar{X_b}) = \mu_a - \mu_b\)；

因此均值差的无偏估计为 \(\bar{X_a} - \bar{X_b}\)。

类似于在 双样本 t 检验 中的思路，我们可以证明：

\[ \frac{(\bar{X_a} - \bar{X_b}) - (\mu_a - \mu_b)}{\sqrt{D(\bar{X_a} - \bar{X_b})}} \sim t(N - k) \]

\[ D(\bar{X_a} - \bar{X_b}) = \sigma^2(\frac{1}{n_a} + \frac{1}{n_b}) \]

其中 \(\sigma^2\) 的无偏估计为：\(\frac{S_E}{N-k}\)。

综上所述，均值差在置信水平为 \(1-\alpha\) 时的置信区间为：

\[ \bar{X_a} - \bar{X_b} \pm t_{1 - \frac{\alpha}{2}, N-k} \sqrt{\frac{S_E}{N-k}(\frac{1}{n_a} + \frac{1}{n_b})}。 \]

LSD 两两比较

方差分析的结果仅能说明各组间均值是否不全相等，若想知晓具体的两组间均值是否相等，则需要使用两两比较的方法。

LSD（least significant difference）是方差分析中常用的两两比较方法之一。对于元素 \(A\) 中的水平 \(a\) 与 \(b\)，组内均值分别为 \(\bar X_a\) 与 \(\bar X_b\)，LSD 的原假设为：\(\bar X_a = \bar X_b\)，备择假设为 \(\bar X_a \neq \bar X_b\)。

我们发现 LSD 的思路与假设等方差的独立双样本 t 检验类似（区别是 LSD 使用了所有样本的联合方差 \(S_E\) 来计算均数差的标准误，而不是两样本的联合方差），根据在上文 计算均值差置信区间 中的推导，LSD 中计算的统计量 t 公式为：

\[ t = \frac{\bar{X_a} - \bar{X_b}}{\sqrt{\frac{S_E}{N - k} (\frac{1}{n_a} + \frac{1}{n_b})}} \]

在显著性水平为 \(\alpha\) 时，当 \(|t| > t_{1 - \frac{\alpha}{2}, N-k}\) 时拒绝原假设，认为两组样本均值不等，否则接受原假设。

2.4.5. 案例

我们现有一份患者年龄的数据数据（如下表所示），这些患者即将分别服用 A 药、B 药与 C 药。在服药之前，我们想先获知各组患者的平均年龄是否显著差异，以避免因年龄不同而导致试验结果的偏倚。我们可以使用方差分析功能来完成上述目的：

年龄	组别

24	A
33	A
35	A
46	A
22	A
36	A
37	B
32	B
23	B
28	B
19	B
32	B
25	C
23	C
44	C
43	C
35	C
38	C

1. 新建一个 “方差分析”，并在 变量 和 组别 列内分别输入上述数据（图 2.134）。

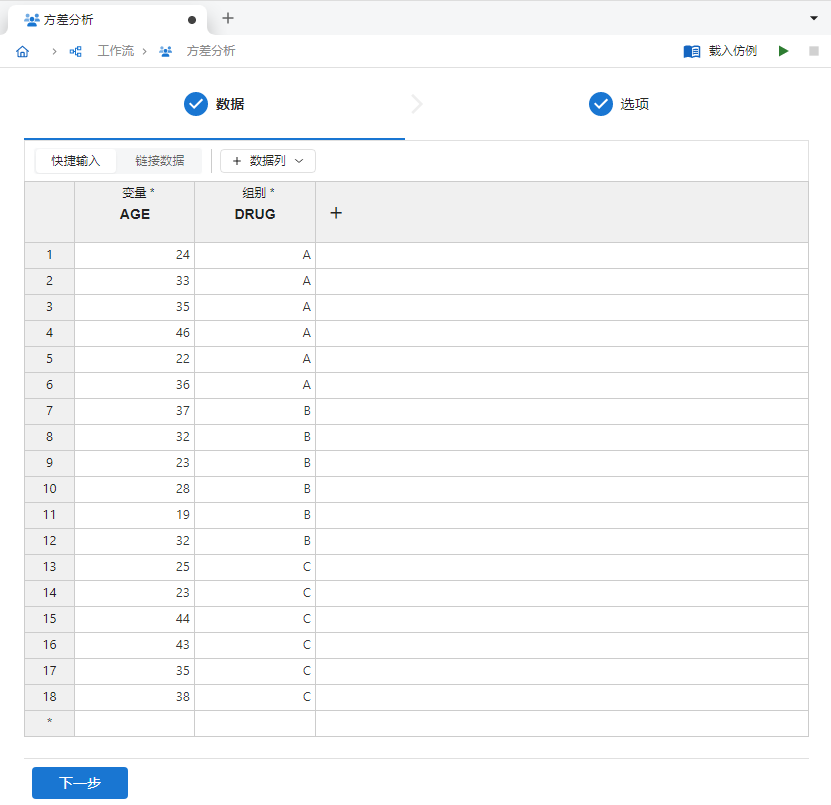
图 2.134 输入数据示意图

2. 数据输入完成后，点击 “下一步” 按钮，在选项页面中选择事后比较方法为 LSD (最小显著性差异法) 以执行两两比较（图 2.135）。

图 2.135 事后比较选项示意图

3. 随后点击 “运行” 按钮执行方差分析。在结果的 “单因素方差分析” 表格（图 2.136）中我们可以获知组间均方为 59.389、统计量 F 值为 0.892、P 值 0.430。因此我们可以认为各组患者间的平均年龄相仿，不存在显著差异。在 “LSD 事后比较” 表格中则可以进一步获知各组的均值差及相关计算结果。

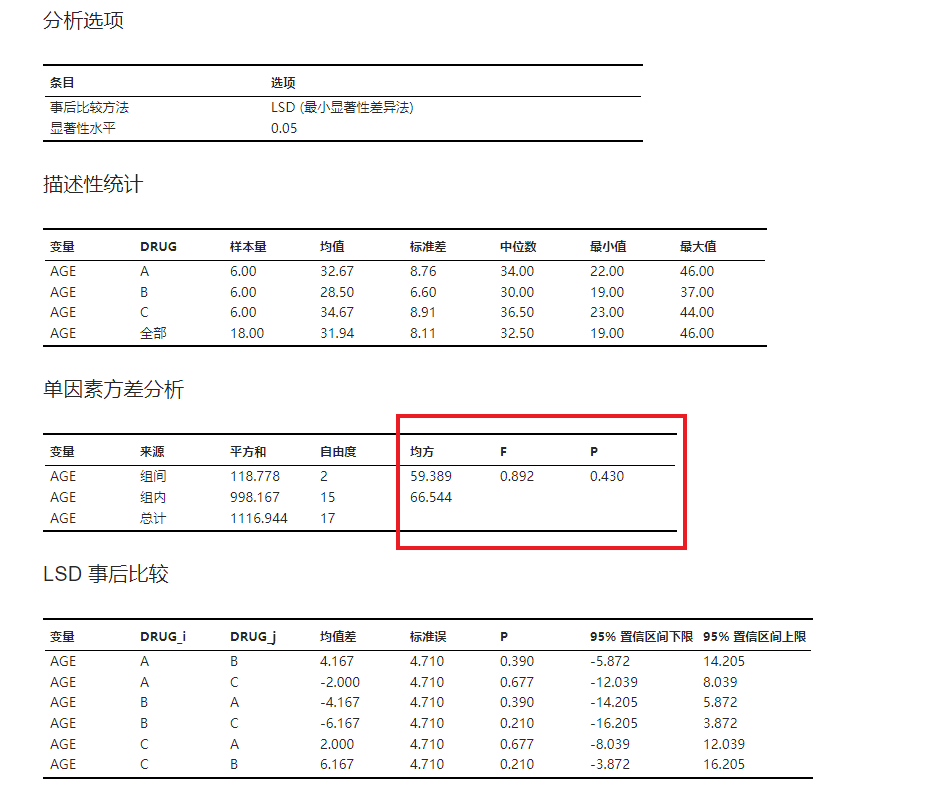
图 2.136 方差分析结果示意图