2.1. 描述性统计#
通过软件内的 “描述性统计” 功能,可以对一组或多组数据进行描述性统计(descriptive statistics)。
描述性统计是一种重要的统计手段,是对数据进行统计分析前的必经步骤之一。通过描述性统计的结果,我们可以观察数据的集中趋势(计算均值与中位数等)与离散程度(计算标准差、方差、四分位数等)。借此我们可以获知数据的整体轮廓、及时发现数据中的离群值并为后续统计分析方法的选择提供帮助。
2.1.1. 数据映射关系#
图 2.98 描述性统计数据映射示意图#
变量 (必选项,多选):需要统计分析的变量数据。
索引 (必选项,多选):数据的索引。拥有相同索引值的数据将被归入同一组;对每组数据将分别进行描述性统计。
2.1.2. 分析选项#
基础统计量#
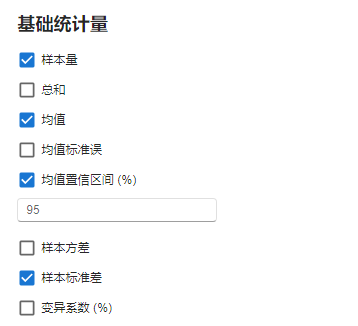
图 2.99 基础统计量选项示意图#
样本量:是否计算变量的样本量(N)。默认勾选。
总和:是否计算变量数据值的总和(sum)。默认不勾选。计算公式为:
均值:是否计算变量数据的均值(mean),也即算数平均数(arithmetic average)。默认勾选。计算公式为:
均值标准误:是否计算变量数据均值的标准误(standard error,SE)。默认不勾选。计算公式为:
均值置信区间(%):是否计算变量数据的均值置信区间(confidence interval,CI)。勾选后需要填入所需计算的区间大小,即 \((1-\alpha) \times 100\%\),默认值为
95(此时 \(\alpha=0.05\))。默认不勾选。计算公式为:
样本方差:是否计算变量数据的样本方差(sample variance,Var)。默认不勾选。计算公式为:
样本标准差:是否计算变量数据的样本标准差(sample standard deviation,SD)。默认勾选。计算公式为:
变异系数(%):是否计算变量数据的变异系数(coefficient of variation,CV)。默认不勾选。计算公式为:
分位数统计量#
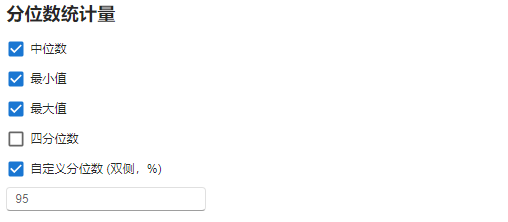
图 2.100 分位数统计量选项示意图#
中位数:是否计算变量数据的中位数(median)。默认勾选。
最小值:是否计算变量数据的最小值(minimum)。默认勾选。
最大值:是否计算变量数据的最大值(maximum)。默认勾选。
四分位数:是否计算变量数据的四分位数(quartiles)。包括下四分位数 Q1(即第 25 百分位数)与上四分位数 Q3(即第 75 百分位数)。默认不勾选
自定义分位数(双侧,%):是否计算自定义百分位数(percentiles)。勾选后填入的数字(下文中记作 \(p\))代表将计算第 \(p\) 个与第 \(100 - p\) 个百分位数,默认 \(p\) 值为
95。默认不勾选。百分位数计算方法如下:
百分位数计算方法
将原数据由小到大排序,假设第 \(p\) 个百分位数位于第 \(i\) 个与第 \(j\) 个数之间(\(j = i + 1\))。先视此时分位数的索引值为 \(i + g\),计算方法如下:
若 \(g > 0\),则取第 \(j\) 个数作为百分位数结果。
若 \(g = 0\),则取第 \(i\) 与第 \(j\) 个数的均值作为百分位数结果。
参考文献:Hyndman, R. J. , & Fan, Y. . (1996). Sample quantiles in statistical packages. American Statistician, 50(4), 361-365.
对数统计量#

图 2.101 对数统计量选项示意图#
对数均值:是否计算对数变量数据的均值。默认不勾选。计算公式如下:
对数标准差:是否计算对数变量数据的标准差。默认不勾选。计算公式如下:
几何均值:是否计算变量数据的几何均值(geometric mean)。默认不勾选。计算公式如下:
几何标准差:是否计算变量数据的几何标准差。默认不勾选。计算公式如下:
几何变异系数(%):是否计算变量数据的几何变异系数。默认不勾选。计算公式如下:
2.1.3. 分析结果#
分析选项#
本次描述性统计所计算的统计量。示例可见 图 2.102。

图 2.102 分析选项表格示意图#
描述性统计#
描述性统计中各统计量的计算结果。示例可见 图 2.103。
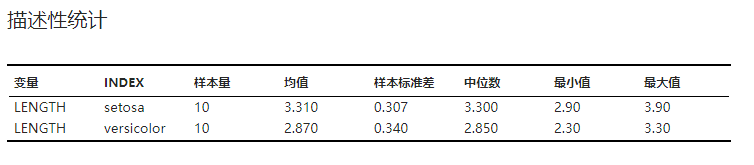
图 2.103 描述性统计表格示意图#
运行日志#
描述性统计运行日志,包含软件版本、运行时间、运行成功与否等信息。示例可见 图 2.104。

图 2.104 运行日志示意图#
2.1.4. 案例#
在对临床试验数据进行分析前,我们往往需要首先获知受试者的基本人口学数据分布特征(如均值、标准差等)才能制订后续的分析计划。使用描述性统计功能可以快速的完成上述分析需求。
例如我们现有如下人口学特征数据(如下表所示),我们欲获取其数据分布特征。
年龄 体重 身高
36 56 170
66 67 166
60 70 168
29 55 172
22 58 167
56 68 168
53 49 175
50 51 181
61 52 156
34 55 160
新建一个 “描述性统计” 分析,新增两个
变量列并输入上述数据,如 图 2.105 所示:
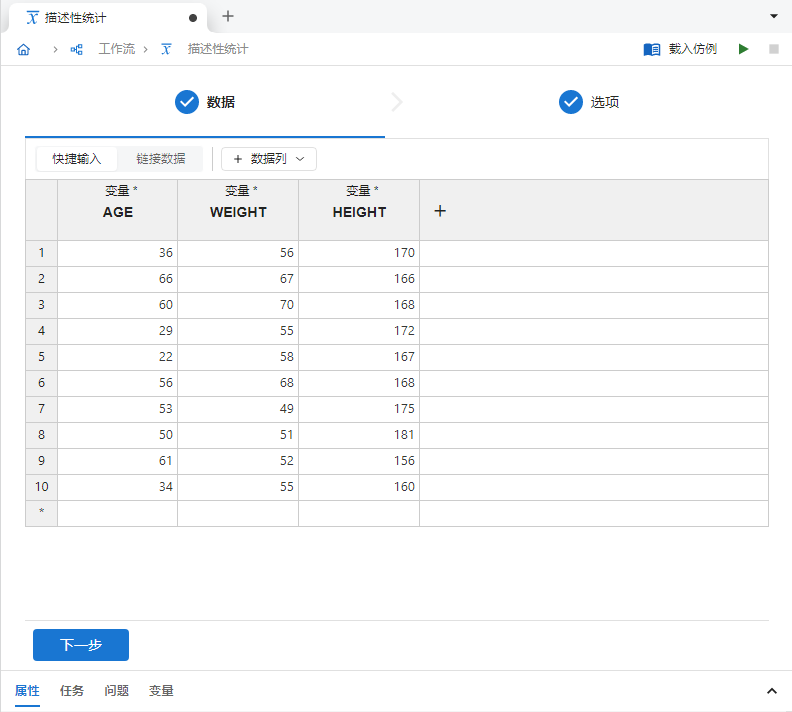
图 2.105 输入数据示意图#
输入完成后,点击 “下一步” 按钮。我们可以勾选所需的统计量,例如此案例中我们勾选
四分位数(图 2.106)。
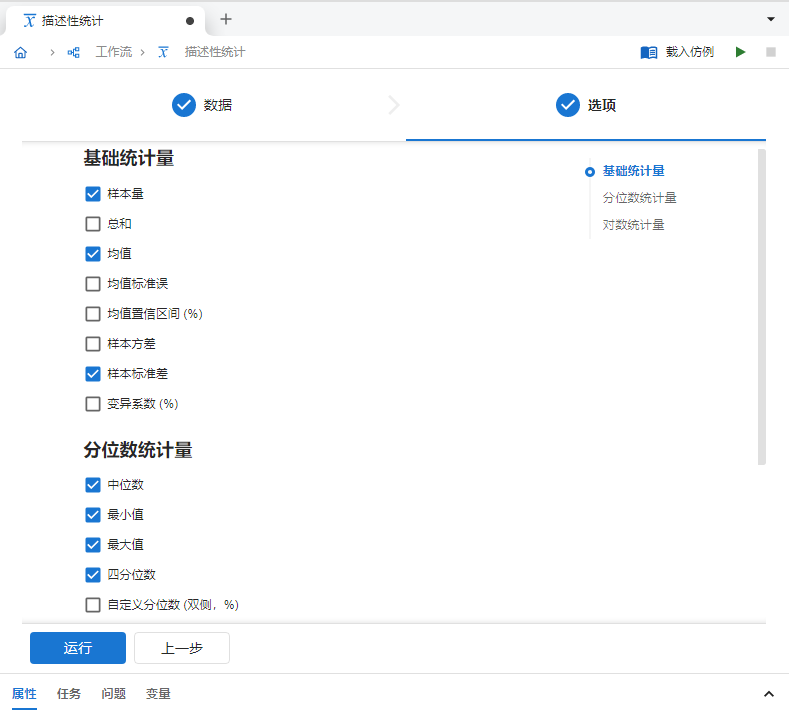
图 2.106 统计量选项示意图#
设置完成后,点击 “运行” 按钮以执行描述性统计。在 “描述性统计” 表格(图 2.107)中我们可以获知年龄、体重与身高的均值分别为 46.7、58.1、168.3;样本标准差为 15.239、7.549、7.072;中位数为 51.5、55.5、168.0;Q1 至 Q3 范围为 (34.0, 60)、(52.0, 67.0)、(166, 172)。
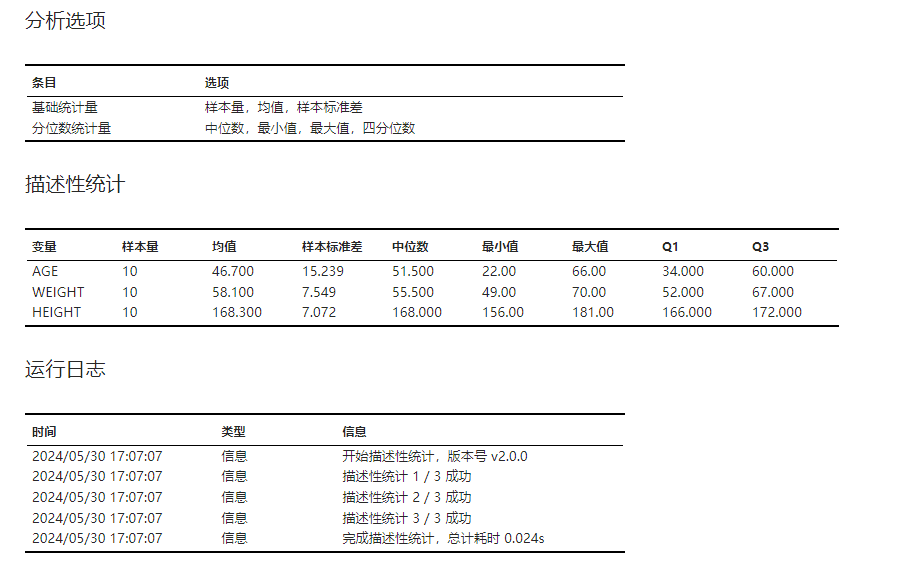
图 2.107 描述性统计结果示意图#
