生存分析

生存分析（survival analysis）是一种在临床研究预后分析中常用的统计学方法。通过生存分析可以获知某个时间点的生存率、生存曲线的变动趋势以及影响生存率的潜在因素。生存分析的常用方法包括 Kaplan–Meier 法与 Cox 回归分析法等。

功能简介

• 若想使用 Kaplan–Meier 法绘制生存曲线并进行组间 Log Rank 检验，可使用 K-M 生存分析（图 487）。

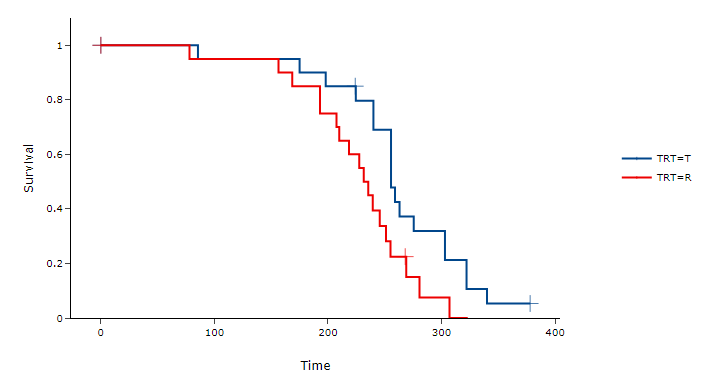
图 487 K-M 生存分析结果示意图

• 若想构建 Cox 比例风险模型并计算各个因素相应的风险比（hazard ratio），可使用 Cox 回归分析（图 488）。

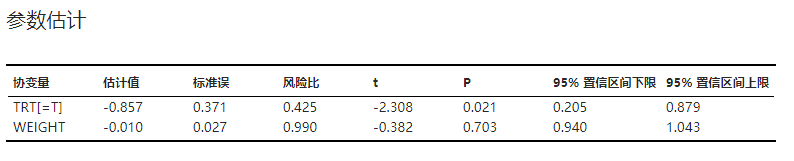
图 488 Cox 回归分析结果示意图

生存分析常用概念

• 事件（events）：指代某种处理措施失败或失效的特征事件，如患者死亡或患者病情恶化。

• 存活（survive）：代表研究对象未发生事件的状态。

• 生存时间（survival time）：研究对象从试验开始直到事件发生所经历的时间。

• 生存率（survival rate）：研究对象从试验开始直到某个特定时间点仍然存活的概率。

• 删失（censoring）：事件发生而未被观测到的情况。常见的产生删失的原因包括失去随访以及研究对象主动退出研究等。

• 生存函数（survival function）：生存率有关于时间的函数。一般记作 \(S(t)\)。

• 风险率（hazard rate）：某时刻下存活的研究对象将要发生事件的概率，风险率越大则发生事件的可能性越大。

• 风险函数（hazard function）：风险率关于时间的函数。一般记作 \(h(t)\)。

• 累计风险函数（cumulative hazard function）：风险率关于时间的积分，代表了在某时刻前发生事件的累计概率。一般记作 \(H(t)\)。

风险函数与生存函数的关系

令随机变量 \(Y\) 表示患者生存时间，定义其在 \(t\) 时间的概率密度函数为 \(f_Y(t)\)，其累积概率密度函数为 \(F_Y(t) = \int_{0}^{t} f_Y(t) dt\)，则有：\(S_Y(t) = 1 - F_Y(t)\)。

根据风险函数定义，可得：\(h_Y(t) = \lim_{\delta t \to 0} \frac{P(t < Y ≤ t + \delta t | Y > t)}{\delta t}\)。

由此可证：

\[\begin{split} h_Y(t) & = \lim_{\delta t \to 0} \frac{P(t < Y ≤ t + \delta t)}{\delta t \times S_Y(t)} \\ & = \lim_{\delta t \to 0} \frac{F_Y(t + \delta t) - F_Y(t)}{\delta t \times S_Y(t)} \\ & = \frac{f_Y(t)}{S_Y(t)} \\ & = \frac{f_Y(t)}{1 - F_Y(t)} \\ & = - \frac{\partial}{\partial t} ln(1 - F_Y(t)) \\ & = - \frac{\partial}{\partial t} ln(S_Y(t)) \end{split}\]

综上所述，生存函数 \(S(t)\) 与风险函数 \(h(t)\) 关系为：

\[ S(t) = exp(- \int_{0}^{t} h(t) dt) = exp(- H(t)) \]