平行设计 ABE 分析#

使用软件内的 “平行设计 ABE 分析” 可对平行试验设计得到的药动学参数数据进行平均生物等效性（average bioequivalence，ABE）分析。一般常用于判断两组半衰期较长的药物间的生物等效性。

若想获知生物等效性研究的背景知识，可参考：生物等效性。

若想获知线性混合效应模型（linear mixed model）相关的模型算法与统计分析理论，可参考：线性混合效应模型。

数据映射关系#

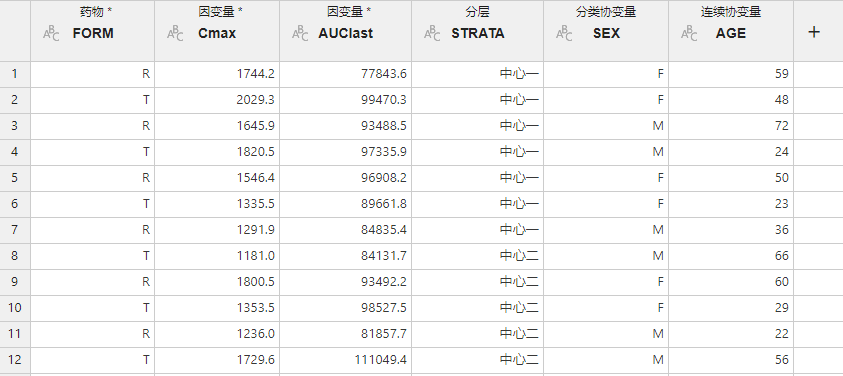
../_images/be-parallel-data-mapping.png

图 380 平行设计 ABE 分析数据映射关系示意图#

  • 因变量 （必选项，多选）：需要分析的因变量，一般为药动学参数数据，如峰浓度 \(C_{max}\) 和 \(AUC_{0-t}\) 等。多个因变量将分别进行建模分析。

  • 药物 （必选项，单选）：受试者接受的药物类别。

  • 分层 （可选项，多选）：数据的分层。不同分层水平的数据将分别独立建模与分析。

  • 分类协变量 （可选项，多选）：其他的分类协变量。

  • 连续协变量 （可选项，多选）：其他的连续协变量。

分析选项#

数据选项#

../_images/be-parallel-data-option.png

图 381 数据选项示意图#

  • 参比制剂：选择在 “药物” 数据中代表参比制剂的值。可选项为 “药物” 数据中所有非重复的项。默认值为 R（如果有）或 “药物” 数据中第一个数据的值。

等效性标准#

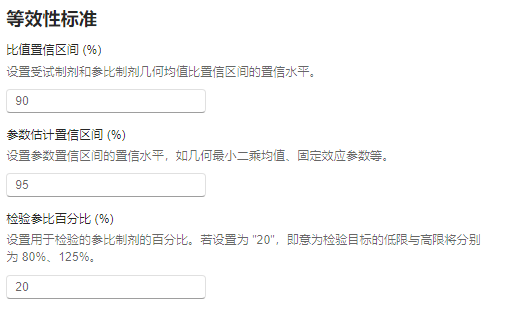
../_images/be-parallel-equivalence-option.png

图 382 等效性标准选项示意图#

  • 比值置信区间 (%)：设置受试制剂与参比制剂几何最小二乘均值比置信区间的置信水平。默认值为 90。

  • 参数估计置信区间 (%)：设置固定效应参数估计值、最小二乘均值、最小二乘均值差、几何最小二乘均值置信区间的置信水平。默认值为 95。

  • 检验参比百分比 (%)：设置用于检验的参比制剂百分比，将影响等效性界值的大小。默认值为 20。

备注

参数置信区间的计算方法可参见 固定效应参数假设检验、最小二乘均值、最小二乘均值差 等小节。

检验参比百分比与等效性界值的关系可参见 生物等效性统计假设 小节。

模型选项#

固定效应#

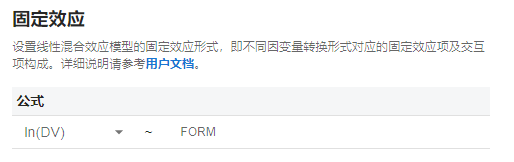
../_images/be-parallel-fixed-effect-model.png

图 383 固定效应选项示意图#

此选项框左侧可选择因变量的转换形式，可选项为 ln(DV) 与 log10(DV)，默认选项为 ln(DV)。

此选项框右侧可输入线性混合效应模型自变量的组合形式，应为原数据中除 “因变量” 外的列名及加号（+）、乘号（*）、分隔符（|）或尖括号（<>）的组合。即决定模型 \(y = X\beta + Z \gamma + \epsilon\) 中 \(X\) 的构建形式，具体方法可参见 矩阵 X 与向量 β 的构建 小节。默认值为 药物 + 分类协变量 + 连续协变量（其中某项若没有相应的映射数据则将被省略）。

加号（+）表示纳入某效应。其余符号则用于表达交互效应：

  • 乘号（A*B）：表示两个变量间的交互效应。等价于 R 语言线性回归模型（lm()）公式中的 A | B。

  • 分隔符（A*B）：表示两个变量的主效应与交互效应，即 A + B + A*B。等价于 R 语言线性回归模型（lm()）公式中的 A * B。

  • 尖括号（A<B>）：表示两个变量间的嵌套关系，在语法上等同于 B * A。

可通过输入 -1 来去除模型中的截距项，例如：

ln(DV) ~ FORM + CONCAV + CATCOV - 1

随机效应#

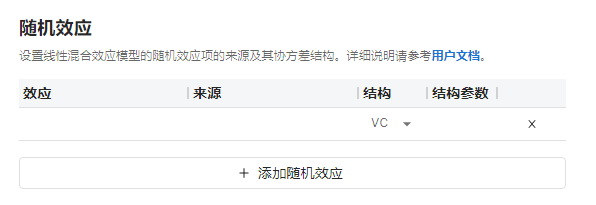
../_images/be-parallel-random-effect-model.png

图 384 随机效应选项示意图#

在此表格中可以为模型添加随机效应，即 \(y = X\beta + Z \gamma + \epsilon\) 中设计矩阵 \(Z\) 的构建形式与 \(\gamma\) 协方差矩阵的类型。

“效应” 与 “来源” 单元格中支持填入数字 1 、除 “因变量” 外的列名、或由加号（+）、乘号（*）、分隔符（|）、尖括号（<>）组成的列名组合。两个单元格中变量的克罗内罗积（kronecker product）将组成设计矩阵 \(Z\)。详情可参见 矩阵 Z 与向量 γ 的构建 小节。

在 “结构” 单元格中可选择随机效应参数向量 \(\gamma\) 的协方差矩阵类型，可选项包括 VC、CS 与 FA0(q)。若选择 FA0(q)，则需要填入其 “结构参数”，默认值为 q=2。协方差矩阵类型相关内容可参见 协方差矩阵结构 小节。

对于平行设计 ABE 分析，默认不添加随机效应项。

点击表格下方的 “+ 添加随机效应” 按钮可以增加一个随机效应。当存在随机效应时，点击每一行右侧的 × 按钮可删去此随机效应。

计算选项#

../_images/be-parallel-calc-option.png

图 385 计算选项示意图#

  • 拟合算法：求解参数所需使用的最优化算法。可选项为 Powell、BObyQA、Nelder-Mead。默认选项为 Powell。

  • 最大迭代次数：最优化算法的最大迭代次数。默认值为 2000。

  • xtol：相对参数收敛界值。当迭代间的参数估计值变更小于此值时即视作参数估计值已收敛。默认值为 1E-6。

  • ftol：相对目标函数（-2LL）的收敛界值。当迭代间的目标函数变更值小于此值时即视作目标函数已收敛。默认值为 1E-6。

  • 奇异性容差：奇异性容差（singularity tolerance）的值。矩阵的特征值（eigen values）若小于这个数值则将被视作等于这个数值，用于避免在求解对数行列式（log determinant）中的数值问题。默认值为 1E-12。

参考文献

优化算法相关参考文献：

  • Powell, M. J. (1964). An efficient method for finding the minimum of a function of several variables without calculating derivatives. The computer journal, 7(2), 155-162.

  • Powell, M. J. (2009). The BOBYQA algorithm for bound constrained optimization without derivatives. Cambridge NA Report NA2009/06, University of Cambridge, Cambridge, 26, 26-46.

  • Nelder, J. A., & Mead, R. (1965). A simplex method for function minimization. The computer journal, 7(4), 308-313.

分析结果#

分析选项#

本次平行设计 ABE 分析所使用的选项设置以及模型形式。示例可见 图 386。

../_images/be-parallel-result-options.png

图 386 分析选项表格示意图#

平均生物等效性#

平均生物等效性计算结果表格，包括受试制剂与参比制剂对应的因变量几何最小二乘均值（对应列名为 Geo LSMean）及其比值。当几何均值比落于生物等效性范围内（一般为 80% - 125%）即可认为两种药物生物等效。结果表格示例可见 图 387。

几何均值比以及把握度的计算方法可参见 生物等效性数据处理与分析 小节。

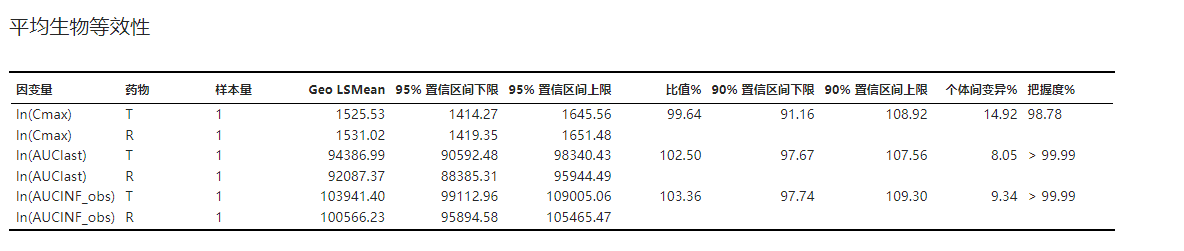
../_images/be-parallel-result-equivalence.png

图 387 平均生物等效性表格示意图#

双单侧 t 检验#

双单侧 t 检验的结果。相关统计理论可见 双单侧 t 检验 小节。示例可见 图 388。

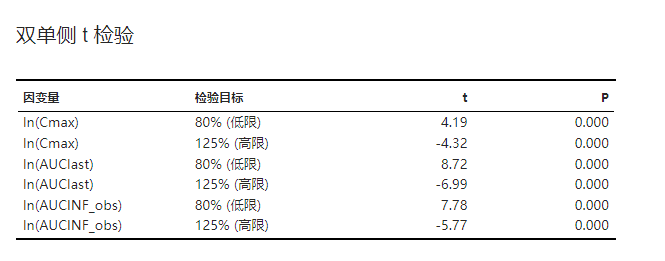
../_images/be-parallel-result-t-test.png

图 388 双单侧 t 检验表格示意图#

Ⅲ 型方差分析#

Ⅲ 型方差分析的结果。相关的算法理论可见 固定效应的方差分析 小节。示例可见 图 389。

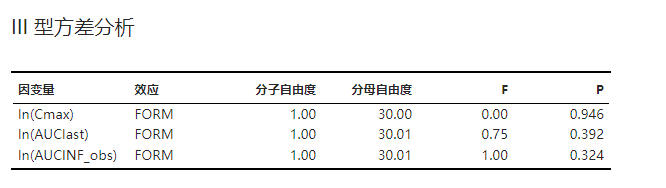
../_images/be-parallel-result-anova.png

图 389 Ⅲ 型方差分析表格示意图#

固定效应参数#

固定效应参数的估计结果，包括参数估计值以及假设检验结果。示例可见 图 390。

线性混合效应模型中固定效应参数的估算方法及其假设检验方法可见 线性混合效应模型似然函数与参数估算 及 固定效应参数假设检验 小节。

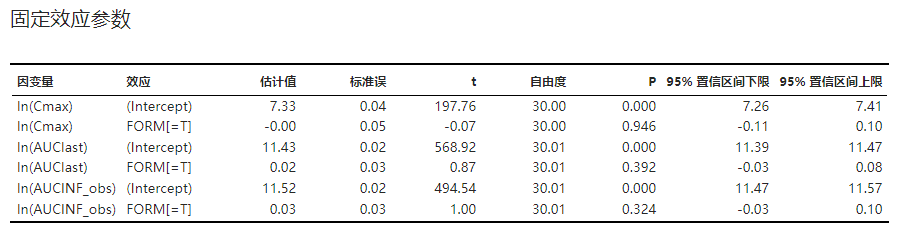
../_images/be-parallel-result-fixed-effect.png

图 390 固定效应参数表格示意图#

协方差参数#

协方差参数的估计结果，包括随机效应参数向量 \(\gamma\) 的协方差矩阵 \(G\) 中的参数以及残差的参数估计结果。示例可见 图 391。

若协方差矩阵结构为 VC，则其中的参数 \(\sigma\) 将被命名为 sigma；若协方差矩阵结构为 CS，则其中的参数 \(\sigma\) 与 \(\sigma_1\) 将被命名为 sigma 与 sigma_1；若协方差矩阵结构为 FA0(q)，则其中的参数 \(\lambda_1^2\)、\(\lambda_2^2\)、\(\lambda_1 \lambda_2\) 等将被命名为 FA0_i_j，其中 i 与 j 为参数所在的行数与列数。

协方差矩阵的构建和结构相关内容可见 设计矩阵与参数向量的构建 小节。

../_images/be-parallel-result-cov-params.png

图 391 协方差参数表格示意图#

最小二乘均值#

受试制剂与参比制剂对应的因变量最小二乘均值及其假设检验结果。示例可见 图 392。

最小二乘均值的计算方法可见 最小二乘均值 小节。

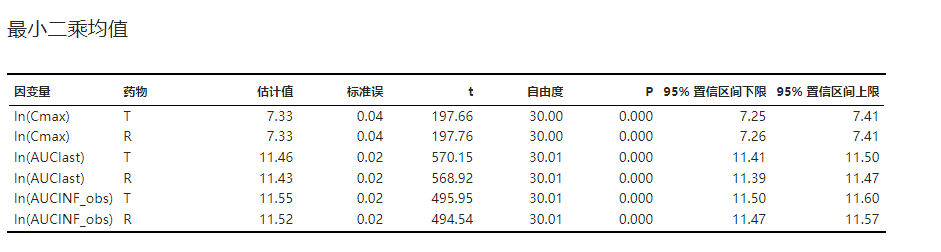
../_images/be-parallel-result-lsmeans.png

图 392 最小二乘均值表格示意图#

最小二乘均值差#

受试制剂与参比制剂因变量最小二乘均值差（mean difference）及其假设检验的结果（此处为与 0 的 t 检验结果）。示例可见 图 393。

../_images/be-parallel-result-mean-diff.png

图 393 最小二乘均值差表格示意图#

个体拟合#

个体拟合结果表格，包括对数观测值、模型预测值及残差，可用于检查模型拟合情况。示例可见 图 394。

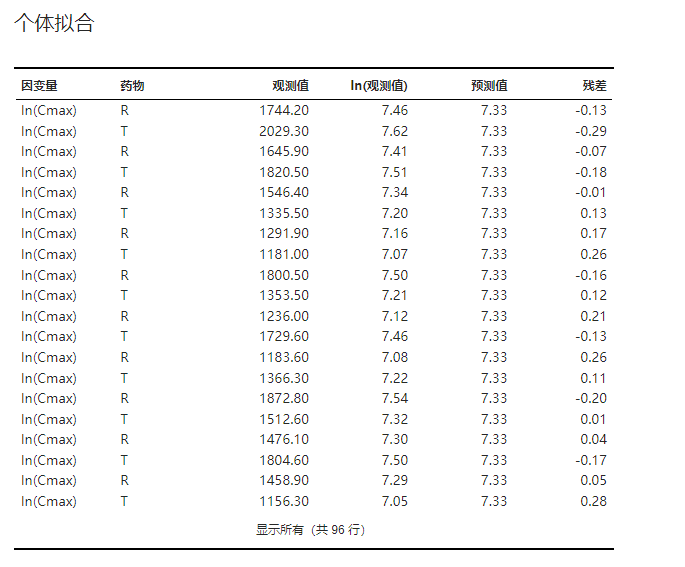
../_images/be-parallel-result-ind-fit.png

图 394 个体拟合表格示意图#

模型诊断#

模型诊断结果表格，包括模型是否收敛、限制极大似然估计算法（restricted maximum likelihood estimate，REML）的对数似然函数值（log likelihood）、目标函数值（即负 2 倍的对数似然函数值，记作 -2LL）、AIC（赤池信息准则，Akaike information criterion） 与 BIC（贝叶斯信息准则，Bayesian Information Criterion）。示例可见 图 395。

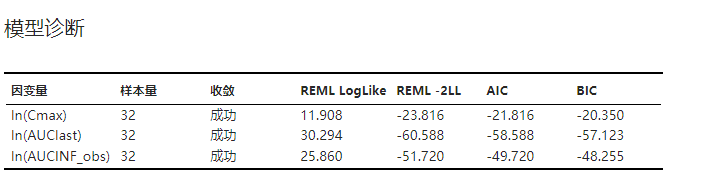
../_images/be-parallel-result-diagnosis.png

图 395 模型诊断表格示意图#

迭代历史#

各个模型的迭代历史，包括最优化过程中各个迭代间的模型目标函数值与协方差参数估计值。示例可见 图 396。

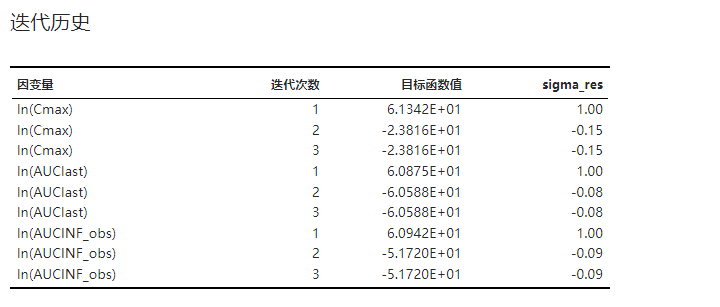
../_images/be-parallel-result-iter-history.png

图 396 迭代历史表格示意图#

运行日志#

平行设计 ABE 分析的运行日志，包含软件版本、各步骤运行时间、运行成功与否、运行过程中的警告信息等内容。示例可见 图 397。

../_images/be-parallel-result-log.png

图 397 运行日志表格示意图#