线性混合效应模型

在本节中，我们将介绍线性混合效应模型（linear mixed model，LMM）的模型基本形式、设计矩阵的构建方法以及相关事后分析的统计理论。

模型基本形式

线性混合效应模型是一种同时包含固定效应（fixed effects）与随机效应（random effects）的统计学模型。相较于传统的线性回归模型，线性混合效应模型通过加入随机效应使得其可以对重复测量的数据以及具有聚集效应的数据进行分析。

例如在生物等效性试验中，由于受试者服药序列的不同，可能导致了某一序列受试者的药动学特征与另一序列不同。此时受试者在序列上有聚集效应，而传统的线性回归模型由于假设样本间互相独立，因而无法解决此类问题。

模型中的固定效应概括了在某些主要变量水平上的数据趋势。这些效应假定对于的研究人群而言是恒定的而非随机的，因此被称作固定效应。固定效应一般由研究者事先约定，主要目的在于对感兴趣的变量的不同水平之间进行比较，例如 ABE 研究中不同药物、序列或周期水平间的药动学参数差异。

随机效应则用于描述样本中个体差异的来源。这些差异往往是因为抽样的样本不同而随机产生的，且无法被已有的固定效应完全解释：例如 ABE 研究中因受试者不同而产生的观测值差异。

此外时常会发生某一变量只能在另一个变量的某个水平内被测量的现象，这样的关系称为嵌套（nested）。在模型构建过程中也需要考虑变量之间是否存在嵌套关系，例如 ABE 研究中我们常认为受试者编号嵌套于序列中。

LMM 模型的基本形式为：

\[ y = X\beta + Z \gamma + \epsilon \]

其中各符号代表：

• \(y\)：因变量观测值。

• \(\beta\)：未知的固定效应参数向量。

• \(\gamma\)：未知的随机效应向量，假定其服从 \(N(0, G)\) 的正态分布，\(G\) 为协方差矩阵。

• \(X\)：将 \(y\) 对应至 \(\beta\) 的已知设计矩阵（design matrix）。

• \(Z\)：将 \(y\) 对应至 \(\gamma\) 的已知设计矩阵。

• \(\epsilon\)：未知的残差向量，假定其服从 \(N(0, R)\) 的正态分布，\(R\) 为协方差矩阵。

设计矩阵与参数向量的构建

矩阵 \(X\) 与向量 \(\beta\)

矩阵 \(X\) 由 0 与 1 构成，其第一列固定为 1 来代表截距项，其余列的取值由固定效应变量的观测值及其变量类型决定。对于分类变量，将生成一个由 0 与 1 组成的哑变量向量代表其各个分类的取值；对于连续变量则取其原观测值。对于存在相互作用或嵌套关系（例如 ID<SEQ>，其也等价于 SEQ*ID）的两个变量，逐行计算哑变量向量及连续变量的克罗内克积（kronecker product），其结果作为设计矩阵 \(X\) 的元素值。

备注

克罗内克积是一种矩阵运算方法，记作 \(\otimes\)。对于 \(X \in \mathbb{R}^{m \times n}\) 与 \(Y \in \mathbb{R}^{p \times q}\)，定义：

\[\begin{split} X \otimes Y = \begin{pmatrix} x_{11}Y & x_{12}Y & \cdots & x_{1n}Y \\ x_{21}Y & x_{22}Y & \cdots & x_{2n}Y \\ \vdots & \vdots & \ddots & \vdots \\ x_{m1}Y & x_{m2}Y & \cdots & x_{mn}Y \end{pmatrix} \in \mathbb{R}^{(mp) \times (nq)} \end{split}\]

例如对于指代药物批次（三分类变量）的哑变量向量为 \(\begin{bmatrix} 1 & 0 & 0 \end{bmatrix}\)，序列（四分类变量）的哑变量向量为 \(\begin{bmatrix} 0 & 0 & 0 & 1\end{bmatrix}\)，两者的克罗内克积为：

\[ \begin{align}\begin{aligned} &\ \quad \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} \otimes \begin{bmatrix} 0 & 0 & 0 & 1 \end{bmatrix}\\&\ = \begin{bmatrix} 1\times0 & 1\times0 & 1\times0 & 1\times1 & 0\times0 & 0\times0 & 0\times0 & 0\times1 & 0\times0 & 0\times0 & 0\times0 & 0\times1 \end{bmatrix}\\&\ = \begin{bmatrix} 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \end{aligned}\end{align} \]

例如对于 2x2 交叉设计的试验，假设固定效应为 序列 + 周期 + 药物，对应的哑变量及设计矩阵 \(X\) 如 图 401 所示：

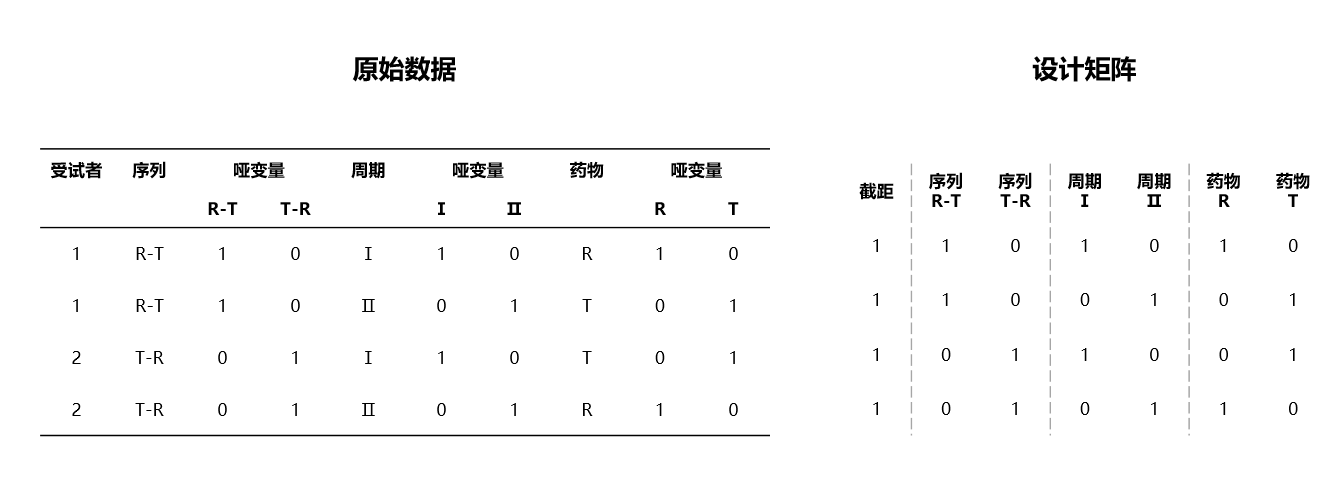
图 401 2x2 交叉设计试验的设计矩阵 \(X\) 示意图

对于 \(m \times n\) 的设计矩阵 \(X\)，相应的 \(\beta\) 为长度是 \(n\) 的向量，其中的元素代表了各变量当前水平的固定效应的大小。

\[ \beta = \begin{bmatrix} \beta_0 & \beta_1 & \cdots & \beta_{n-1} \end{bmatrix} \]

矩阵 \(Z\) 与向量 \(\gamma\)

设计矩阵 \(Z\) 的构造方式与 \(X\) 类似，由 “效应” 变量以及 “来源” 变量的克罗内克积构成。例如当随机效应设置如同 图 402 时，其对应的 \(Z\) 矩阵如 图 403 所示：

图 402 随机效应设置示意图

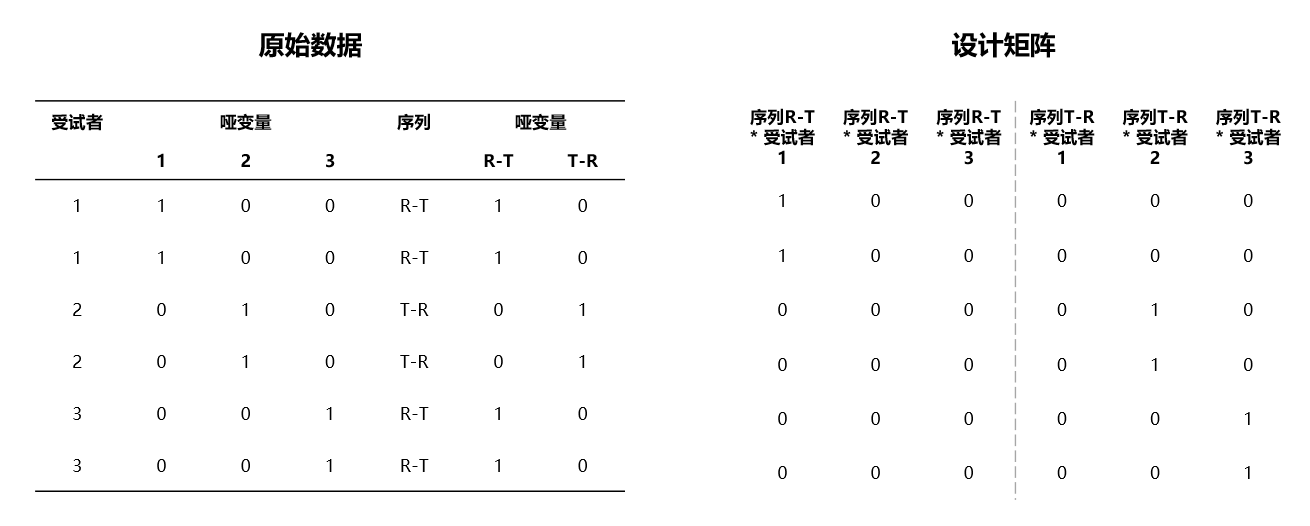
图 403 设计矩阵 \(Z\) 示意图

与 \(\beta\) 的构造类似，对于 \(m \times n\) 的设计矩阵 \(Z\)，相应的 \(\gamma\) 为长度是 \(n\) 的向量：

\[ \gamma = \begin{bmatrix} \gamma_1 & \gamma_2 & \cdots & \gamma_n \end{bmatrix} \]

\(\gamma\) 的方差-协方差矩阵 \(G\) 为 \(n \times n\) 的矩阵，其具体形式由指定的 协方差矩阵结构 决定。当在模型中指定 \(k\) 个随机效应时，它们将各自构建 \(k\) 个设计矩阵 \(Z_k\) 与协方差矩阵 \(G_k\)，且以如下形式组成模型整体的 \(Z\) 与 \(G\) 矩阵：

\[\begin{split} Z = \begin{bmatrix} Z_1 \\ Z_2 \\ \vdots \\ Z_k \end{bmatrix} \end{split}\]

\[\begin{split} G = \begin{bmatrix} G_1 & & & \\ & G_2 & & \\ & & \ddots & \\ & & & G_k \\ \end{bmatrix} \end{split}\]

矩阵 \(R\)

假设共有 \(n\) 个观测值，则 \(\epsilon\) 是长度为 \(n\) 的代表残差大小的向量。当未指定重复效应时，对应的 \(R\) 矩阵为：

\[ R = \sigma^2 I_n \]

其中 \(I_n\) 为大小是 \(n \times n\) 的单位阵。

当模型中存在重复效应时，首先根据 “来源” 以及 “效应” 变量的水平值将原数据依次排序，此时 \(R\) 为：

\[ R = \Sigma \]

\(\Sigma\) 为 \(n \times n\) 的协方差矩阵。\(\Sigma\) 具体形式由指定的 协方差矩阵结构 决定。

当重复效应中有 \(g\) 个 “组别” 时，每个组别分别构建 \(R_g\) 矩阵，模型整体的 \(R\) 矩阵为：

\[\begin{split} R = \begin{bmatrix} R_1 & & & \\ & R_2 & & \\ & & \ddots & \\ & & & R_g \\ \end{bmatrix} \end{split}\]

例如当重复效应设置如 图 404 所示时，对应的 \(R\) 矩阵可见 图 405：

图 404 重复效应设置示意图

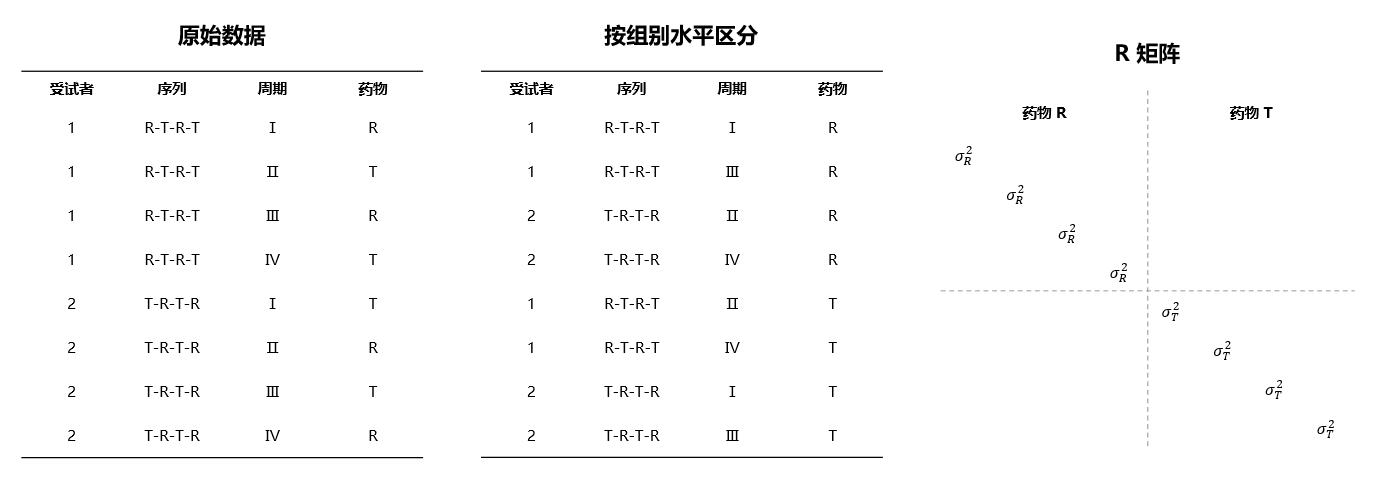
图 405 \(R\) 矩阵示意图

协方差矩阵结构

结构	全称	参数数量	示例
VC	Variance Components	g	\(\begin{bmatrix} \sigma_A^2 & & & \\ & \sigma_A^2 & & \\ & & \sigma_B^2 & \\ & & & \sigma_B^2 \end{bmatrix}\)
CS	Compound Symmetry	2	\(\begin{bmatrix} \sigma^2 + \sigma_1 & \sigma_1 & \sigma_1 & \sigma_1 \\ \sigma_1 & \sigma^2 + \sigma_1 & \sigma_1 & \sigma_1 \\ \sigma_1 & \sigma_1 & \sigma^2 + \sigma_1 & \sigma_1 \\ \sigma_1 & \sigma_1 & \sigma_1 & \sigma^2 + \sigma_1 \end{bmatrix}\)
FA0(q)	No Diagonal Factor Analytic	\(\frac{q}{2}(2t - q - 1)\)	\(\begin{bmatrix} \lambda_1^2 & \lambda_1 \lambda_2 & 0 & 0 \\ \lambda_2 \lambda_1 & \lambda_2^2 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}\)

在随机效应中，\(g\) 为随机效应的个数，\(t\) 为 “效应” 变量的水平数，\(q\) 为 FA0(q) 方法的结构参数；在重复效应中 \(g\) 为 “组别” 变量的水平数。

似然函数与参数估算

对于 LMM 模型，我们使用限制极大似然估计算法（restricted maximum likelihood estimate，REML）来计算其参数估计值。

在传统的极大似然估计过程中（maximum likelihood estimate，MLE），往往先估计固定效应参数，再以此为基准估计 \(Var(y)\)，依次迭代上述过程直至似然函数收敛至最大值。MLE 算法的主要缺点为其未考虑在估算时由于固定效应 \(\beta\) 所引起的自由度减少的问题，所以其方差估计值是有偏的。而 REML 的基本思想是找到一个满秩的矩阵 \(A\) 来使得 \(A' \times y\) 服从均值为 0 的正态分布，从而可以不对 \(\hat{\beta}\) 进行计算并利用 MLE 算法得到方差的无偏估计，随后采用线性代数方法即可求解对应的 \(\hat{\beta}\)。

以下公式中符号 \(|\quad|\) 代表矩阵的行列式；\('\) 代表矩阵的转置；\(^{-1}\) 代表矩阵的逆。

\(y\) 的方差表达式如下：

\[ V = Var(y) = ZGZ' + R \]

对于其中的未知矩阵 \(G\) 与 \(R\)，REML 的对数似然函数为：

\[ \mathscr{l}(G, R) = -\frac{1}{2} log |V| - \frac{1}{2} log |X'V^{-1}X| - \frac{1}{2} r'V^{-1}r - \frac{n-p}{2} log(2\pi) \]

其中 \(r = y - X(X'V^{-1}X)^{-1} X'V^{-1}y\)；\(p\) 为矩阵 \(X\) 的秩。

通过最优化算法可以求得使目标函数 \(-2\mathscr{l}(G, R)\) 最小的 \(\hat{G}\) 与 \(\hat{R}\)。根据以下方程组可以解得 \(\hat{\beta}\) 与 \(\hat{\gamma}\)：

\[\begin{split} \begin{bmatrix} X'\hat{R}^{-1}X & X'\hat{R}^{-1}Z \\ Z'\hat{R}^{-1}X & Z'\hat{R}^{-1}Z + \hat{G}^{-1} \end{bmatrix} \begin{bmatrix} \hat{\beta} \\ \hat{\gamma} \end{bmatrix} = \begin{bmatrix} X'\hat{R}^{-1}y \\ Z'\hat{R}^{-1}y \end{bmatrix} \end{split}\]

\[ \hat{\beta} = (X'\hat{V}^{-1}X)^{-1} X'\hat{V}^{-1}y \]

\[ \hat{\gamma} = \hat{G}Z'\hat{V}^{-1}(y - X\hat{\beta}) \]

参考文献

线性混合效应模型似然函数与参数估计相关参考文献：

• Helen, B. , & Robin, P. . (2006). Applied Mixed Models in Medicine, Second Edition. John Wiley & Sons, Ltd.

• Ramon, C. L. , George, A. M. , Walter, W. S. , Russell, D. W. , & Oliver, S. . (2006). SAS® for Mixed Models, Second Edition. Cary, NC: SAS Institute Inc.

固定效应参数假设检验

类似于线性回归对回归系数的假设检验，若固定效应向量 \(\beta\) 长度为 \(n\)，对其中某个固定效应参数 \(\beta_k\) 做假设检验的原假设与备择假设为：

\[ \begin{align}\begin{aligned} &\ H_0: \beta_k = 0\\&\ H_1: \beta_k \neq 0 \end{aligned}\end{align} \]

固定效应参数估计值 \(\hat{\beta}\) 的方差估计值 \(\hat{C}\) 为：

\[ \hat{C} = (X'\hat{V}^{-1}X)^{-1} \]

所以对于某一个固定效应参数估计值 \(\hat{\beta}_k\) 其方差估计值即为 \({I\hat{C}I'}_{kk}\)。其中 \(I\) 为大小是 \(n \times n\) 的单位阵。构建检验统计量 \(t\)：

\[ t = \frac{\hat{\beta}_k}{\sqrt{{I\hat{C}I'}_{kk}}} \sim t_v \]

其中 \(v\) 为利用 Satterthwaite 法 计算得到的自由度。当显著性水平为 \(\alpha\) 时，若 \(|t| > t_{\frac{\alpha}{2}, v}\) 时则拒绝原假设。

Satterthwaite 自由度

当存在复杂的协方差矩阵时，独立样本方差线性组合的有效自由度不能简单地通过独立样本及其衍生量的个数计算得到。而 Satterthwaite 法（也被称为 Welch–Satterthwaite equation）是一种通过计算近似分布的自由度来估计独立样本方差线性组合自由度的方法。

假设有 \(n\) 个样本方差 \(s^2_i\)，\(i = (1, 2, \cdots n)\)，其自由度分别为 \(v_i\)，它们的线性组合服从卡方分布：

\[ \chi^2 = \sum_{i=1}^n k_i s^2_i \]

其中 \(k_i\) 是任意正实数，一般为 \(\frac{1}{v_i + 1}\)。Satterthwaite 认为上述卡方分布近似分布的自由度为：

\[ v ≈ \frac{(\sum_{i=1}^n k_i s^2_i)^2}{\sum_{i=1}^n \frac{(k_i s^2_i)^2}{v_i}} \]

若将其应用于 LMM 模型，当固定效应与随机效应参数向量 \(\theta\) 长度为 1 时，其方差自由度可以表示为：

\[ v = \frac{2({I\hat{C}I'})^2}{g'Ag} \]

其中 \(g\) 为在 \(\hat{\theta}\) 处 \(I\hat{C}I'\) 对 \(\theta\) 的梯度；\(A\) 为 \(\hat{\theta}\) 的协方差矩阵。

当 \(\theta\) 长度不为 1 时：

\[ \begin{align}\begin{aligned} &\ v_j = \frac{2(d_j)^2}{{g'}_j A g_j}\\&\ E = \sum_{j=1}^{r_{I'\hat{C}I}} \frac{v_j}{v_j - 2}\\&\ v = \frac{2E}{E - r_I} \end{aligned}\end{align} \]

其中 \(d_j\) 为矩阵 \(I'\hat{C}I\) 的第 \(j\) 个特征值，\(U\) 为其特征向量构成的矩阵；记矩阵 \(UI\) 的第 \(j\) 行为 \(b_j\)，\(g_j\) 是在 \(\hat{\theta}\) 处 \(b_j\hat{C}b_j'\) 对 \(\theta\) 的梯度；\(r_{I'\hat{C}I}\) 与 \(r_I\) 分别为矩阵 \(I'\hat{C}I\) 与 \(I\) 的秩。

参考文献

更多相关信息可参考以下文献：

• Satterthwaite, F. E. . (1946). An approximate distribution of estimates of variance components. Biometrics Bulletin, 2 (6): 110–114.

最小二乘均值

最小二乘均值（least squares means）可以视作某一效应的边际均值（marginal means）。对于 LMM 模型而言，即控制某一固定效应变量水平得到的因变量预测值均值。在实际建模分析过程中，最小二乘均值可以比较在同一条件下某固定效应水平变化导致的预测值差异大小。

其计算的核心在于构建参考表格（reference grid）\(L\)，继而求解 \(L\hat{\beta}\) 即为各固定效应水平的最小二乘均值。构建 \(L\) 的步骤如下：

1. 若有 \(p\) 个固定效应变量，第 \(i\) 个变量的水平数记作 \(g_i\)（连续变量水平数为 1，取值为其均值），则每个变量有 \(g_i\) 个由 0 与 1 组成的哑变量代表其不同的水平值。对应的 \(L\) 为大小是 \(\sum_{i=1}^p g_i \times \sum_{i=1}^p g_i\) 的表格，其每一行代表计算某一变量水平对应的最小二乘均值时其余变量哑变量的应取值。

2. 假设当前计算变量 \(A\) 的第 \(k\) 个水平对应的最小二乘均值，则此行中代表变量 \(A\) 的第 \(k\) 个哑变量取值为 1，其余与 \(A\) 有关的哑变量取 0。

3. 此行中不涉及变量 \(A\) 的其余变量各个哑变量取值均为 \(\frac{1}{g_i}\)。

4. 若将表示 \(A\) 与其他变量交互作用的变量记作 \(A \times B\)（\(B\) 的总水平数记作 \(g_B\)），则 \(A \times B\) 中与 \(A\) 的第 \(k\) 个水平有关的列取值为 \(\frac{1}{g_B}\)，其余列取 0。

假设固定效应为 药物 + 周期 + 药物*周期，其中 药物 为二分类变量，周期 为三分类变量。则 \(L\) 表格如 图 406 所示：

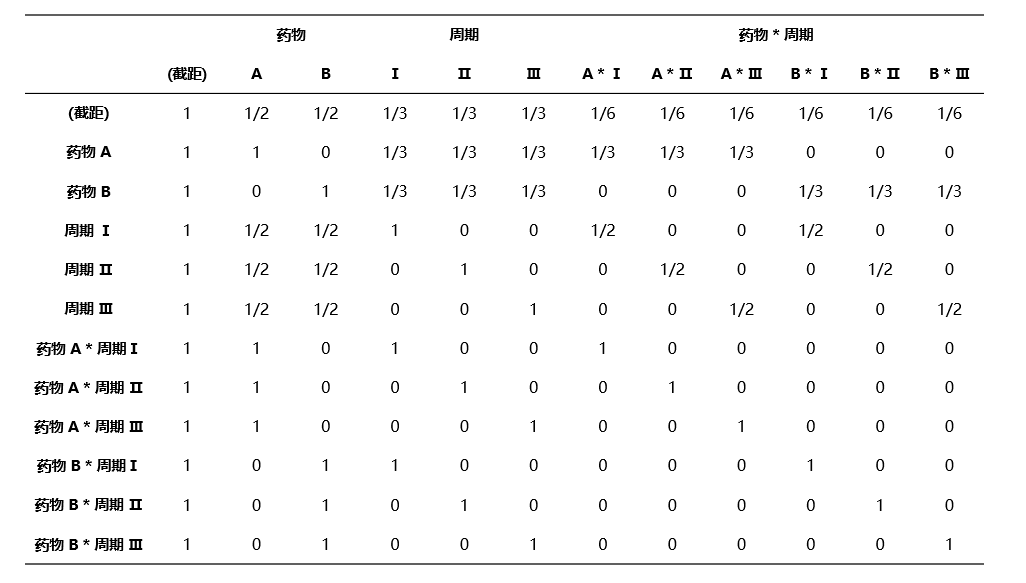
图 406 参考表格 \(L\) 示意图

上述方法也可以用线性代数的形式表示：

1. 对原数据集按照固定效应变量水平进行去重，得到子数据集 \(G\)。

2. 以 \(G\) 为数据构建所有固定效应变量的设计矩阵 \(X\)。

3. 同时以 \(G\) 为数据构建某一固定效应变量 \(A\) 的设计矩阵 \(D\)。

4. 逐列计算 \(D\) 的元素总和，记作向量 \(s\)；并计算 \(w = 1 / s\)。

5. 计算变量 \(A\) 的参考表格 \(L_A = (D \odot w)' X\)。

6. 计算各个变量的参考表格，合并即可得到最终的 \(L\)。

假设计算 药物 变量的参考表格，计算过程中的各矩阵值及最终参考表格可参见 图 407 与 图 408：

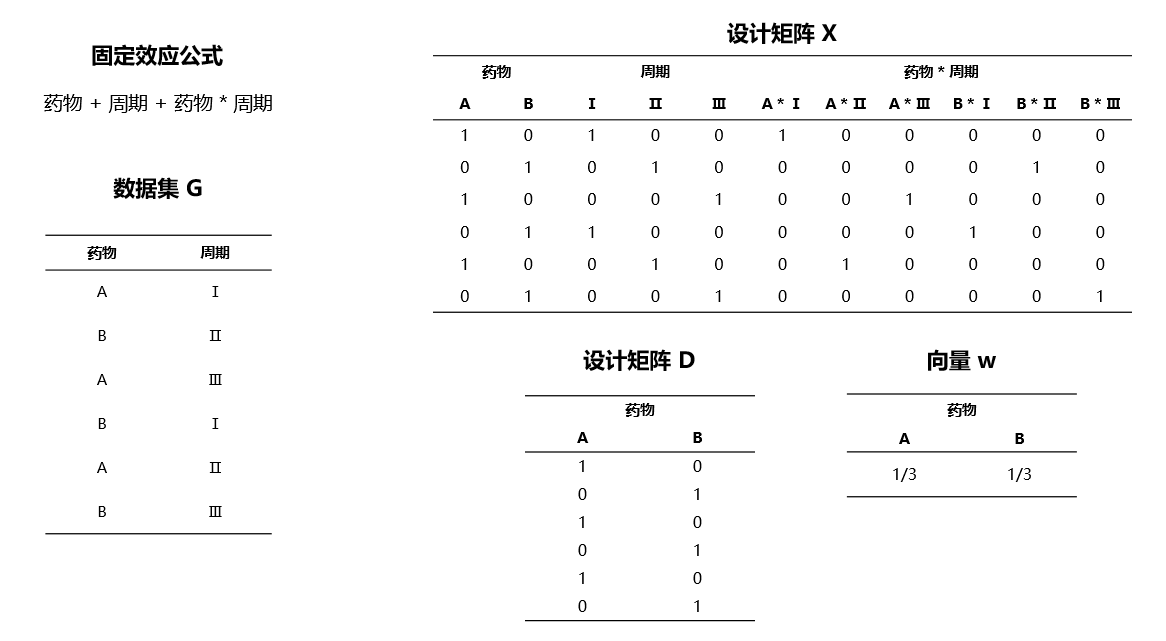
图 407 线性代数法计算参考表格过程中的矩阵值示意图

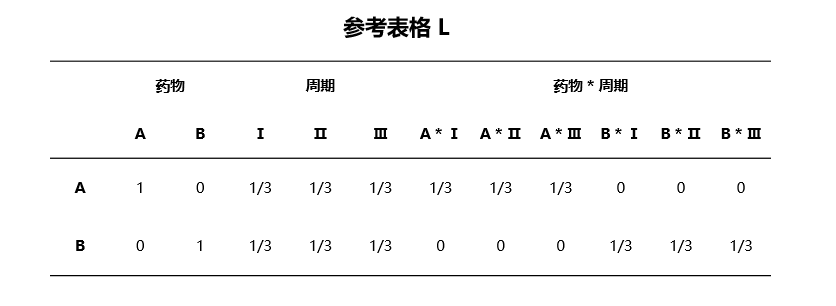
图 408 线性代数法计算的药物变量参考表格值示意图

最小二乘均值的标准误由 \(L\hat{C}L'\) 给出，其假设检验统计量为 \(t = \frac{L \hat{\beta}}{\sqrt{{L\hat{C}L'}}}\)，自由度使用 Satterthwaite 法 近似得到。相关检验方法可参见 固定效应参数假设检验 小节。

最小二乘均值差

最小二乘均值差（mean difference）统计检验的核心思想是：对于某多水平固定效应变量 \(A\)，当模型中仅保留其某一个水平 \(k\) 的效应并扣除另一个水平 \(j\) 的效应，检验此时的最小二乘均值差是否为 0 即可判断两个水平的效应大小是否有显著差异。对于生物等效性试验，则将检验受试制剂与参比制剂的最小二乘均值差是否落于生物等效性界值内。

类似于 最小二乘均值 的计算方法，我们同样需要构建参考表格 \(L\)。对于多水平固定效应变量 \(A\)，构建 \(L\) 的步骤如下：

1. 若模型中共有 \(p\) 个固定效应变量，第 \(i\) 个变量的水平数记作 \(g_i\)（连续变量水平数为 1），每个变量有 \(g_i\) 个哑变量代表其不同的水平值。对于变量 \(A\)，则 \(L\) 大小为 \(C_{g_A}^2 \times \sum_{i=1}^p g_i\)。

2. \(L\) 中的每一行将用于计算水平 \(k\) 与另一个水平 \(j\) 的最小二乘均值差。因此在每一行内将代表水平 \(k\) 的哑变量值设置为 1；代表水平 \(j\) 的哑变量值设置为 -1。

\(L\) 构建完成后，最小二乘均值差的标准误由 \(L\hat{C}L'\) 得到。假设检验统计量为 \(t = \frac{L \hat{\beta}}{\sqrt{{L\hat{C}L'}}}\)，自由度使用 Satterthwaite 法 近似得到。

例如对于固定效应 药物 + 周期，其中 药物 为二分类变量，周期 为四分类变量。当分析 周期 中各水平的最小二乘均值差时，\(L\) 如 图 409 所示：

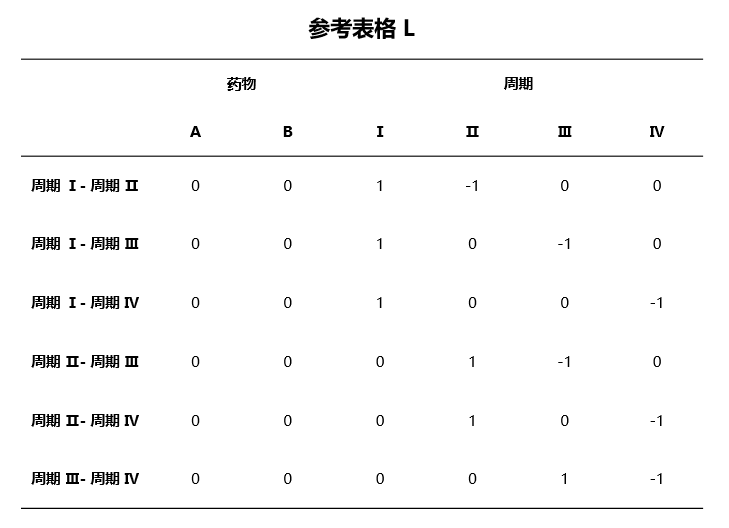
图 409 最小二乘均值差中参考表格示意图

固定效应的方差分析

LMM 模型的各类方差分析的核心假设检验思想是比较在加入或剔除某个固定效应后，模型对因变量的残差平方和（sum of squares，SS）是否有显著差异，以此来判断每个固定效应的贡献是否显著。

Ⅰ 型方差分析

在 Ⅰ 型方差分析中，固定效应将按指定顺序依次引入模型并逐个计算新引入的效应对总变异的贡献。例如对于模型 \(y \sim A + B + A*B\)，我们将先计算只引入效应 \(A\) 时的残差平方和 \(SS(A)\)，随后计算在已引入效应 \(A\) 的情况下再引入 \(B\) 后的残差平方和 \(SS(B|A)\)（式子的右边代表将要被考察的效应，左边代表已引入的效应，下同），最后计算在引入 \(A\) 与 \(B\) 的情况下交互效应 \(A*B\) 的残差平方和 \(SS(A*B | A, B)\)。

Ⅰ 型方差分析计算简单且容易解释每个固定效应的贡献度大小，但其对固定效应的引入顺序敏感，更适用于有明确先后次序的实验设计。

Ⅱ 型方差分析

在 Ⅱ 型方差分析中，将先排除模型中的交互效应并计算每个固定效应的贡献，随后再考虑交互效应的贡献。例如对于模型 \(y \sim A + B + A*B\)，将先计算 \(SS(A | B)\) 以及 \(SS(B |A)\)，最后考虑交互效应的残差平方和 \(SS(A*B | A, B)\)。

Ⅱ 型方差分析不容易受引入顺序的影响，但在计算主效应的贡献时忽略了一部分交互效应，因此其更适用于不包含交互效应的模型。

Ⅲ 型方差分析

在 Ⅲ 型方差分析中，将计算在考虑其他所有效应时剔除某固定效应后的残差平方和来判断每个固定效应的独立贡献。例如对于模型 \(y \sim A + B + A*B\)，效应 \(A\) 的贡献是否显著可以通过残差平方和之比 \(\frac{SS(B, A*B | A, B, A*B)}{SS(A, B, A*B)}\) 来决定（对于效应 \(B\) 以及 \(A*B\) 同理）。

相较于 Ⅰ 型或 Ⅱ 型方差分析，Ⅲ 型方差分析适用于所有类型的实验设计而无需考虑效应引入的先后次序；此外也可以分析交互作用在模型中的贡献程度。

对于上述问题，我们可以进一步将其转化为一个等价的命题：在不考虑其他效应的情况下，某固定效应贡献是否为零？也即当模型中仅包含一个固定效应变量时，其固定效应参数向量 \(\beta\) 均值是否为 0。所以 Ⅲ 型方差分析中假设检验的原假设为：

\[ H_0: \mu_{\beta} = 0 \]

当固定效应变量为多水平分类变量时，其固定效应参数向量 \(\beta\) 长度不为 1。对于多元正态样本的均值检验，我们构建统计量 \(F\)：

\[ \begin{align}\begin{aligned} &\ t^2 = \frac{(P'L \hat{\beta})^2}{d}\\&\ F = \frac{\sum_{j=1}^q t^2_j }{q} \sim F(q, v) \end{aligned}\end{align} \]

上式中 \(L\) 为设计矩阵；\(d\) 与 \(P\) 分别为矩阵 \(L'\hat{C}L\) 的特征值与特征向量；\(\hat{\beta}\) 为原模型固定效应参数估计值向量。

统计量 \(F\) 服从自由度为 \(q\) 与 \(v\) 的 F 分布。其中 \(q\) 为固定效应水平数；\(v\) 为 Satterthwaite 自由度，计算方法可见 Satterthwaite 自由度 小节。当 \(F ≥ F(q, v)\) 时拒绝原假设，认为此固定效应参数向量均值为 0，其对模型变异的解释性较低。

设计矩阵 \(L\) 的构建方法与 最小二乘均值 中参考表格的构建方法类似，核心思想为仅保留将进行方差分析的固定效应变量并排除模型中的其他固定效应，构建步骤如下：

1. 若模型中共有 \(p\) 个固定效应变量，第 \(i\) 个变量的水平数记作 \(g_i\)（连续变量水平数设为 1），则每个变量有 \(g_i\) 个由 0 与 1 组成的哑变量代表其不同的水平值。若方差分析研究的变量为 \(A\)，则 \(L\) 为大小是 \(g_A \times \sum_{i=1}^p g_i\) 的表格。

2. 对于变量 \(A\) 的第 \(k\) 个水平，\(L\) 的第 \(k\) 行中代表此水平的哑变量取值为 1，其余列均取 0，依此类推。

例如对于固定效应 药物 + 周期，其中 药物 为二分类变量，周期 为四分类变量。当对 周期 进行 Ⅲ 型方差分析时，\(L\) 如 图 410 所示：

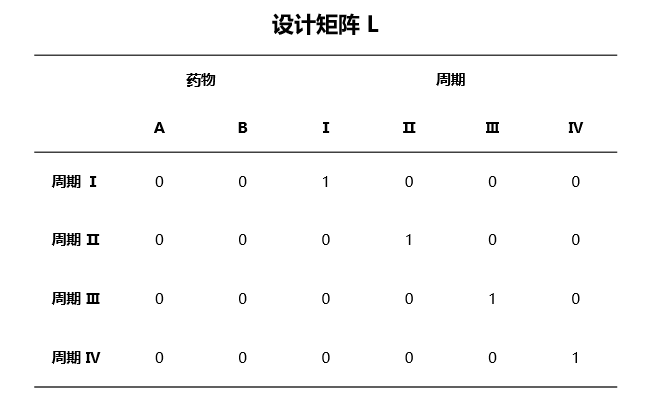
图 410 Ⅲ 型方差分析中设计矩阵 \(L\) 示意图