2.2. 单样本 t 检验#
通过软件内的 “单样本 t 检验” 功能,可以对一组数据进行单样本 t 检验(one-sample t-test)。
单样本 t 检验一般用于检验一组总体方差未知但符合正态分布的数据的均值是否与已知的总体均值相等。
2.2.1. 数据映射关系#
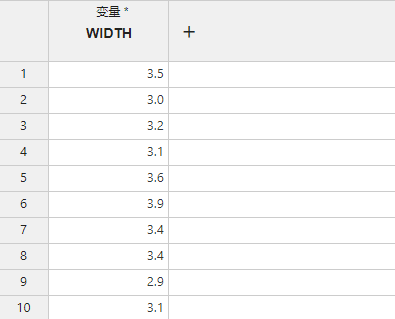
图 2.108 单样本 t 检验数据映射示意图#
变量 (必选项,多选):需要检验的变量数据。若有多个变量,则将分别进行检验。
2.2.2. 分析选项#
计算选项#
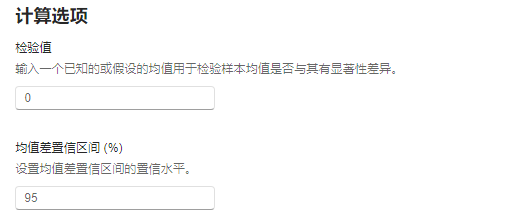
图 2.109 计算选项示意图#
检验值:总体均值。具体假设检验过程可参考:统计理论 小节。默认值为
0。均值差置信区间(%):均值差置信区间的置信水平。默认值为
95。计算方法如下:
均值差置信区间计算方法
设样本均值为 \(\bar X\),总体均值为 \(\mu\),均值差计算方法为:
记输入的置信水平为 \(P\),则均值差置信区间 \(CI\) 的计算方法如下:
2.2.3. 分析结果#
分析选项#
本次单样本 t 检验的分析选项设置。示例可见 图 2.110。
图 2.110 分析选项表格示意图#
描述性统计#
被分析变量的描述性统计表格,包括均值、标准差、中位数等。示例可见 图 2.111。

图 2.111 描述性统计表格示意图#
单样本 t 检验#
变量单样本 t 检验结果,包括均值差、统计量 t 值、假设检验 P 值及均值差置信区间等结果。示例可见 图 2.112。

图 2.112 单样本 t 检验表格示意图#
运行日志#
单样本 t 检验运行日志,包含软件版本、运行时间、运行成功与否等信息。示例可见 图 2.113。

图 2.113 运行日志示意图#
2.2.4. 统计理论#
双侧单样本 t 检验的原假设为:样本均值 \(\bar X\) 与总体均值 \(\mu\) 相等;
其备择假设为:样本均值 \(\bar X\) 与总体均值 \(\mu\) 不相等。
计算的统计量为 \(t\),计算公式为:
若假设检验置信水平为 \(\alpha\),数据自由度 \(df = N - 1\),在双侧检验时记 t 分布中界值为 \(t_{\frac{\alpha}{2}, df}\)。当 \(|t| > t_{1 - \frac{\alpha}{2}, df} \) 时则拒绝原假设,认为样本均值 \(\bar X\) 与总体均值 \(\mu\) 不等,否则接受原假设。
2.2.5. 案例#
例如我们有一批糖尿病患者的 BMI(身体质量指数,body mass index)数据,如下表所示:
BMI
32.1
21.6
30.5
25.3
23.0
22.6
22.0
26.2
32.1
30.0
18.6
28.0
23.7
26.2
24.0
现在我们想研究这批患者是否有超重的趋势,可以将上述数据与总体均值(BMI = 24)进行单样本 t 检验,在软件内操作步骤如下:
新建一个 “单样本 t 检验” 分析,并在
变量列内输入上述数据(图 2.114)。
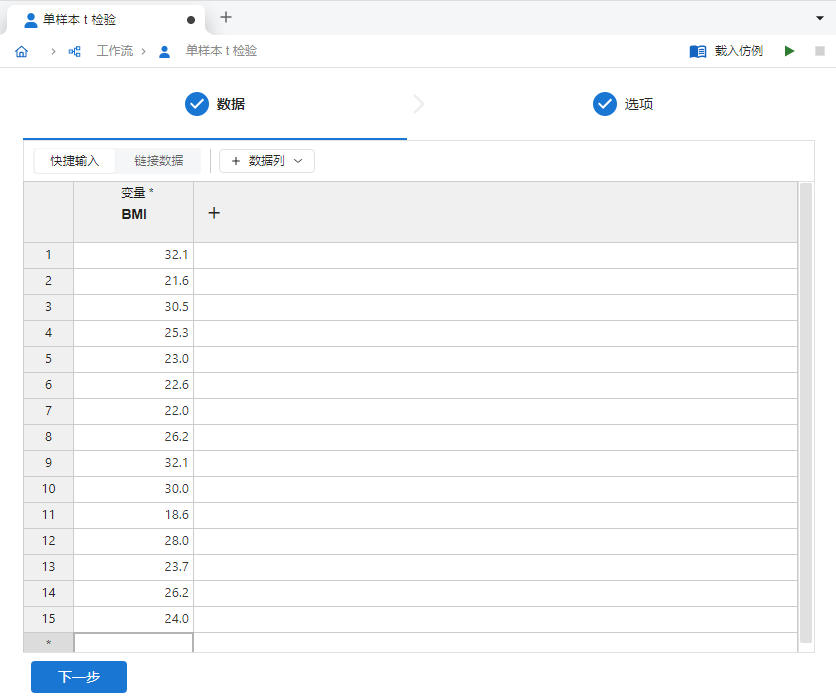
图 2.114 输入数据示意图#
输入完成后,点击 “下一步” 按钮,在选项页面中的 “检验值” 输入框内填入欲检验的总体均值,即
24(图 2.115)。
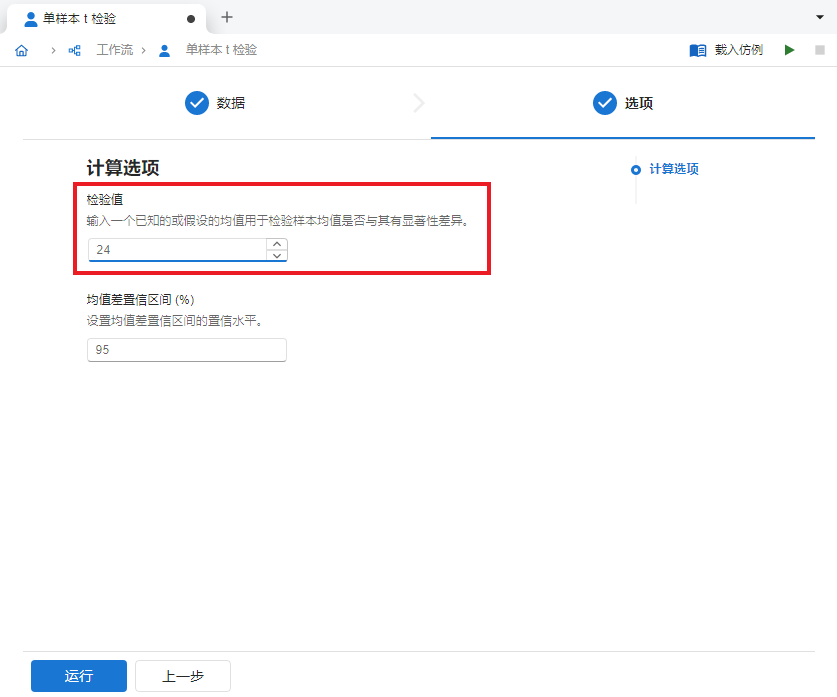
图 2.115 输入检验值示意图#
设置完成后,点击 “运行” 按钮即可执行单样本 t 检验。在结果的 “单样本 t 检验” 表格中(图 2.116),我们可以发现样本均值与总体均值差为 1.727,统计量 t 值为 1.635,假设检验 P 值为 0.124。由于 P 值大于 0.05,我们可以认为这组患者没有超重趋势。

图 2.116 检验结果示意图#
