5.2. 线性回归模型#
使用软件内的 “线性回归模型” 功能,我们可以对多个自变量与因变量构建多元线性回归模型(multiple linear regression model)以解释自变量对因变量变化的影响。
5.2.1. 数据映射关系#
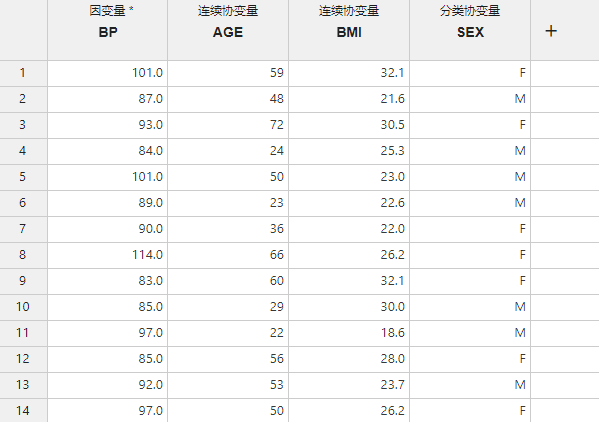
图 5.64 线性回归模型数据映射示意图#
因变量 (必选项,多选):线性回归模型的因变量。如果有多个因变量则将分别对其构建线性回归模型。
连续协变量(可选项,多选):线性回归模型中的连续型协变量(自变量)。
分类协变量(可选项,多选):线性回归模型中的分类型协变量(自变量)。对于此类变量,将分别计算各个分类的回归系数(regression coefficient)。
5.2.2. 分析选项#
模型选项#
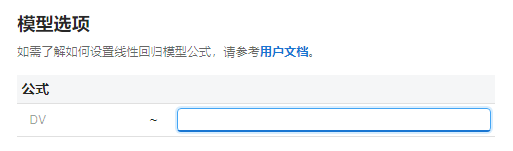
图 5.65 模型选项示意图#
在此选项内的输入框内指定多元线性回归模型自变量的组合形式,应为 “连续协变量” 或 “分类协变量” 列名以及加号(+)的组合。也即填入回归模型 \(Y = b_0 + b_1 x_1 + \cdots + b_p x_p + \epsilon\) 中 \(x_1, x_2, \cdots, x_p\) 的部分。向量 \(x_1, x_2, \cdots, x_p\) 取值于数据集中与其同名的数据列。
例如对于以下数据(图 5.66):
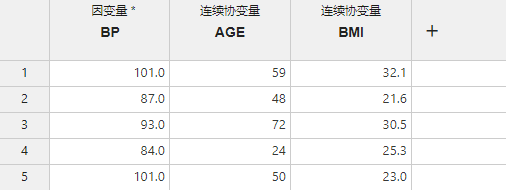
图 5.66 模型选项数据示例#
在 “模型选项” 内输入以下自变量组合形式:AGE + BMI(图 5.67)
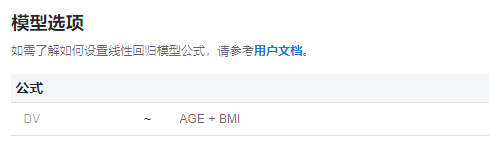
图 5.67 模型选项模型公式示例#
此时正规方程组(定义详见 回归系数的估算 小节)中的各矩阵为:
备注
上述回归模型等同于 R 代码:
lm(formula = BP ~ AGE + BMI)
小技巧
特别地,如果你想在回归模型中去除回归系数 \(b_0\)(截距),可以在模型公式中输入 -1。
例如:AGE + BMI - 1。
计算选项#

图 5.68 计算选项示意图#
回归系数置信区间 (%):设置回归系数估计值置信区间的置信水平。例如输入
95即计算回归系数估计值的 95% 置信区间。相关计算方法可参见 回归系数的假设检验 小节。默认值为95。
5.2.3. 分析结果#
分析选项#
本次线性回归模型的分析选项设置,包括模型公式等。示例可见 图 5.69。

图 5.69 分析选项表格示意图#
参数估计#
多元线性模型回归系数的估计值以及对其假设检验的结果。估算方法与假设检验相关内容可参见 回归系数的估算 与 回归系数的假设检验 小节。示例可见 图 5.70。
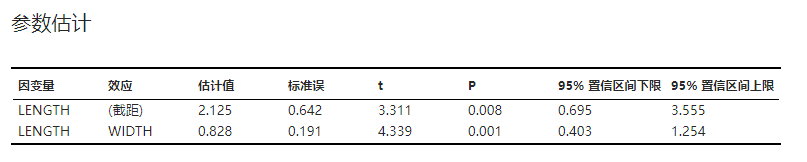
图 5.70 参数估计表格示意图#
模型诊断#
当前多元线性回归模型诊断结果,包括确定系数 \(R^2\)(coefficient of determination,一般被称作 R 方)与调整 \(R^2\)。计算方法可见 确定系数的计算 小节。示例可见 图 5.71。

图 5.71 模型诊断表格示意图#
模型拟合#
当前模型的拟合情况,包括因变量观测值、预测值及残差。示例可见 图 5.72。
其中残差计算公式为 \(\epsilon_i = y_i - \hat{y_i}\)。Pearson 残差即标准化残差(normalized residuals),其计算公式为 \(\epsilon_i / \hat{\sigma}\)。
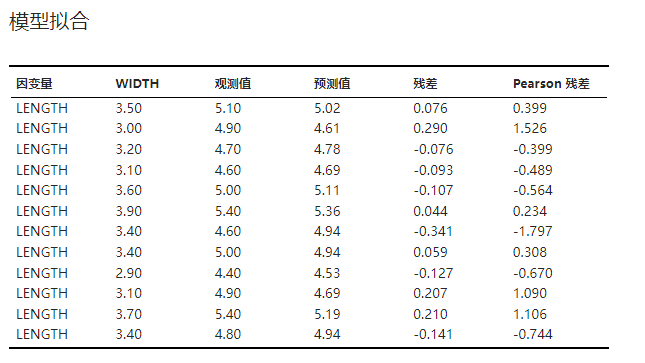
图 5.72 模型拟合表格示意图#
运行日志#
线性回归模型的运行日志,包含软件版本、运行时间、模型拟合成功与否等信息。示例可见 图 5.73。
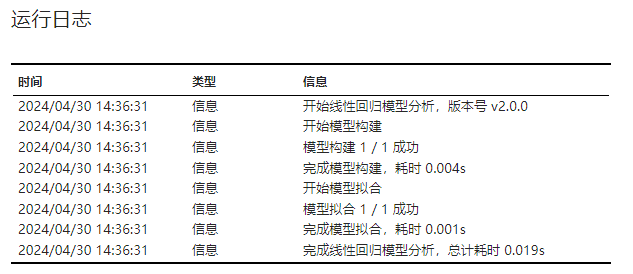
图 5.73 运行日志示意图#
5.2.4. 统计理论#
多元线性回归模型的定义#
随机变量 \(Y\) 往往与多个普通变量(有确定的取值)\(x_1, x_2, \cdots, x_p (p>1)\) 有关。当 \(Y\) 的期望存在且是 \(x_1, x_2, \cdots, x_p\) 的线性函数时,可以写为:
上式被称作多元线性回归模型,其中各个未知参数 \(b\) 称为回归系数;\(\epsilon\) 代表随机误差,且 \(\epsilon \sim N(0, \sigma^2)\)。
回归系数的估算#
假设 \((x_{11}, x_{12}, \cdots, x_{1p}, y_1), \cdots, (x_{n1}, x_{n2}, \cdots, x_{np}, y_n)\) 是一个样本,可以使用最小二乘法来估计参数值。即找到一组参数估计值 \(\hat{b_0}, \hat{b_1}, \cdots, \hat{b_p}\),当 \(b_0=\hat{b_0}, b_1=\hat{b_1}, \cdots, b_p=\hat{b_p}\) 时,可以使残差平方和 \(Q\) 达到最小。
要使得 \(Q\) 最小,则应令 \(Q\) 关于 \(b_0, b_1, \cdots, b_p\) 的偏导数均为 0:
以上偏微分方程组可以改写为:
为了求解上述方程组(常被称为正规方程组,normal equations)中的参数,我们定义如下矩阵:
此时,偏微分方程组可以改写为 \(\boldsymbol{X}^T \boldsymbol{X} \boldsymbol{B} = \boldsymbol{X}^T \boldsymbol{Y}\),通过移项我们就可以得到参数的解 \(\boldsymbol{\hat B}\):
通过高斯-马尔可夫定理(Gauss-Markov assumptions)可以证明 \(\boldsymbol{\hat B}\) 就是 \(\boldsymbol{B}\) 的最佳线性无偏估计量。
一般将 \(\hat{b_0} + \hat{b_1} x_1 + \cdots + \hat{b_p} x_p\) 记作 \(\hat y\)。
回归系数的假设检验#
回归系数的假设检验原假设为 \(b_i = 0\),备择假设为 \(b_i \neq 0\)(当回归系数为 0 时,说明这个自变量对因变量没有显著的解释作用)。我们在下文中将尝试构造对应的检验统计量 \(t\)。
残差平方和 \(Q = \sum_{i=1}^n (y- \hat y)^2\),可以证明(相关证明过程请见下方参考文献):
所以 \(\frac{Q}{n-p}\) 是 \(\sigma^2\) 的一个无偏估计量,记作 \(\hat{\sigma^2}\)。
由于参数估计 \(\boldsymbol{\hat B} \sim N(\boldsymbol{B}, \sigma^2(\boldsymbol{X}^T \boldsymbol{X})^{-1})\),对于其中的任意分量 \(\hat{b_i}\) 则有 \(\hat{b_i} \sim N(b_i, \sigma^2[(\boldsymbol{X}^T \boldsymbol{X})^{-1}]_{ii})\),此时可构造统计量:
当假设检验显著性水平为 \(\alpha\) 时,若 \(|t| > t_{1-\frac{\alpha}{2}, n-p}\) 则拒绝原假设,认为自变量对因变量有显著的解释作用;否则接受原假设。
参考文献
盛骤, 谢式千, & 潘承毅. (2008). 概率论与数理统计(第四版). 高等教育出版社.
确定系数的计算#
确定系数 \(R^2\) 常用于判断线性回归的拟合结果,其值代表了当前回归模型解释了多少因变量中的变异。\(R^2\) 越接近于 1 则说明模型拟合效果越好。其公式如下:
但从上式可以发现,\(R^2\) 对自变量数目的变动不敏感:即使不断加入冗余的自变量,\(R^2\) 也不会变动。所以统计学家们提出了调整 \(R^2\) 的概念,以明确加入新的自变量是否能有效增加模型拟合度,其公式如下:
调整 \(R^2\) 的取值范围同样为 \([0, 1]\),其值越接近 1 就说明模型拟合越好。
5.2.5. 案例#
在本例中,我们将使用内置的糖尿病患者数据集来构建随机血糖(GLU)与部分生理指标的多元线性模型,以发掘糖尿病致病的危险因素。
右键左侧 “数据集” 选项,在右键菜单中选择 “载入仿例数据”;随后在弹出的窗口中单击 “糖尿病患者数据集” 以导入内置仿例数据。导入完成后的数据集如 图 5.74 所示,各列分别代表患者年龄、性别、身体质量指数(body mass index,BMI)、血压(blood pressure,BP)、随机血糖、血清总胆固醇(total cholesterol,TC)、低密度脂蛋白(low density lipoprotein,LDL)与高密度脂蛋白(high density lipoprotein,HDL)。
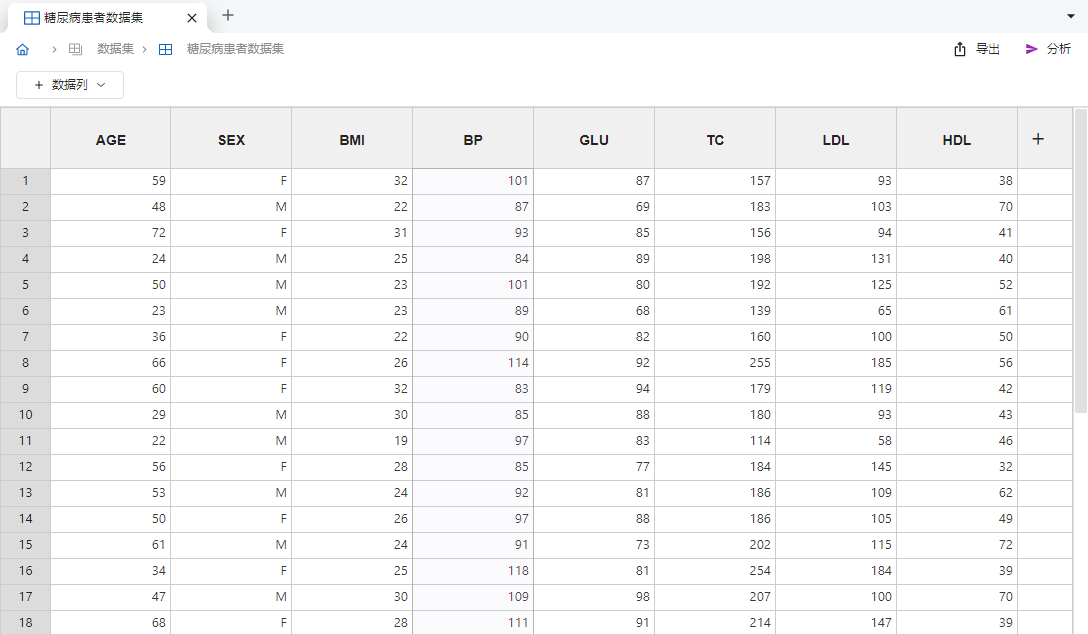
图 5.74 糖尿病患者仿例数据示意图#
新建一个 “线性回归模型” 分析,并在 “链接数据” 模式中选择载入的 “糖尿病患者数据集”。随后将
GLU映射至 “因变量”,SEX映射至 “分类协变量”,其余列映射至 “连续协变量”(除 LDL 与 HDL 列外,因为 TC 与其强相关。为了避免共线性问题,暂不纳入回归模型),如 图 5.75 所示。
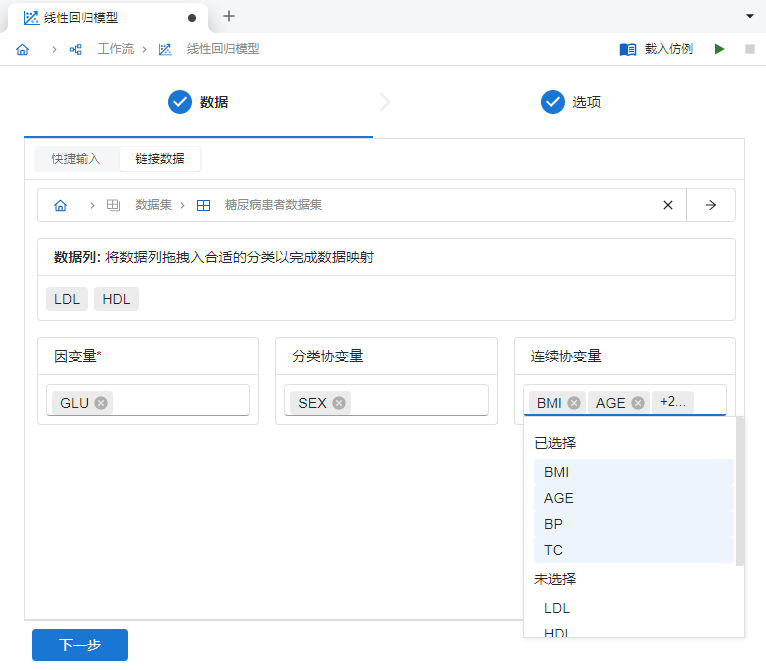
图 5.75 线性回归模型数据映射示意图#
映射完成后,点击 “下一步” 按钮,随后在 “模型选项” 中输入多元线性回归模型公式:
SEX + BMI + AGE + BP + TC(图 5.76)。
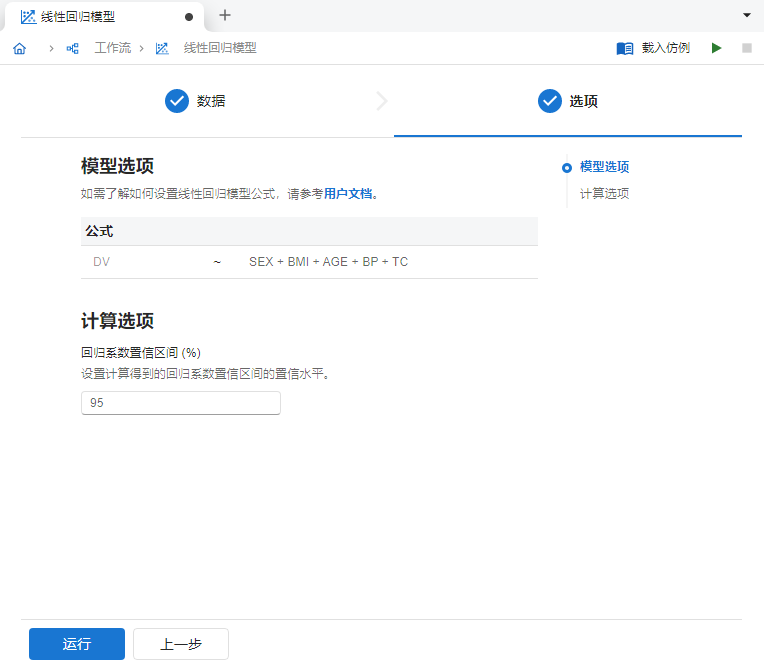
图 5.76 模型公式示意图#
公式输入完成后,点击 “运行” 按钮即可拟合回归模型。在分析结果的 “参数估计” 表格中(图 5.77),我们可以获取各个回归系数的估算值与假设检验结果。我们发现,BMI 对应的回归系数为 0.895,说明 BMI 与血糖值呈正相关。且假设检验 P 值为 0.04,所以我们可以认为肥胖是导致糖尿病的高危因素之一。
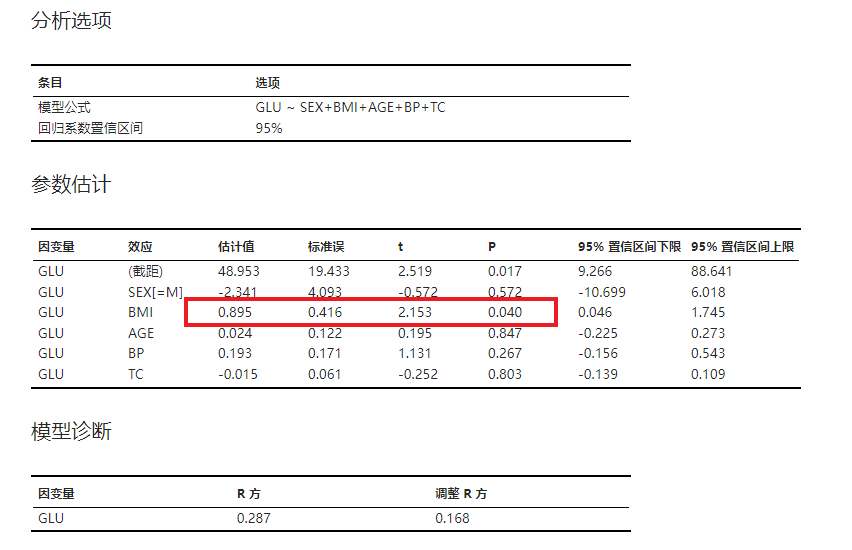
图 5.77 回归模型分析结果示意图#
对于拟合完成的回归模型,我们可以使用软件内的 “散点图” 功能来可视化检验模型的拟合度:新建一个 “散点图”,随后在 “链接数据” 内选择此前线性回归模型结果的 “模型拟合” 表格。随后将
Obs(观测值) 与Pred(预测值)列分别映射至 “X 轴” 与 “Y 轴”,如 图 5.78 所示:
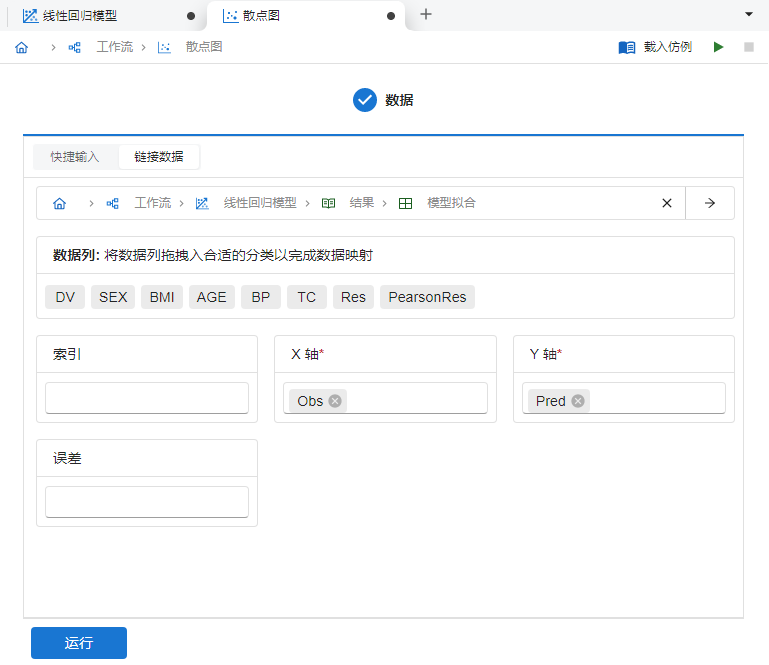
图 5.78 散点图数据映射示意图#
映射完成后点击 “运行” 按钮即可绘制散点图。绘制完成后,我们可以在 “散点图” 选单中修改 “辅助线” 选项为
y = x以绘制一条对角辅助线(图 5.79)。 随后我们进一步在 “坐标轴” 选单中调整 X 轴与 Y 轴坐标轴范围至相同大小(图 5.80)。以上设置完成后,我们发现观测值与预测值基本平均分散于对角辅助线两侧,可以认为模型拟合效果较好。
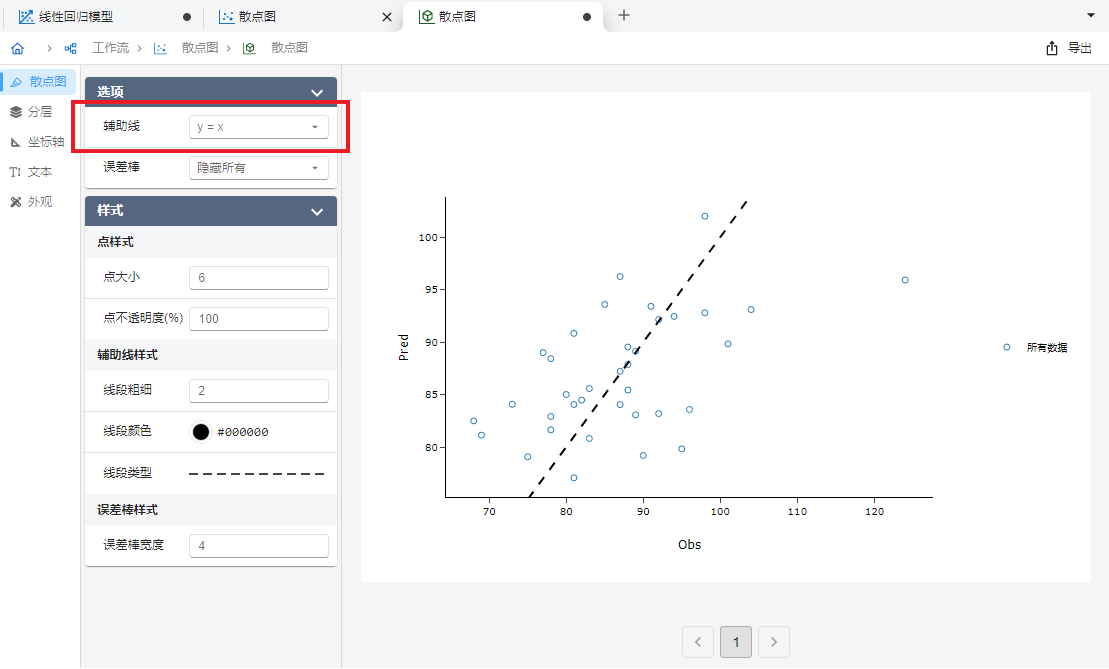
图 5.79 设置 y=x 辅助线示意图#
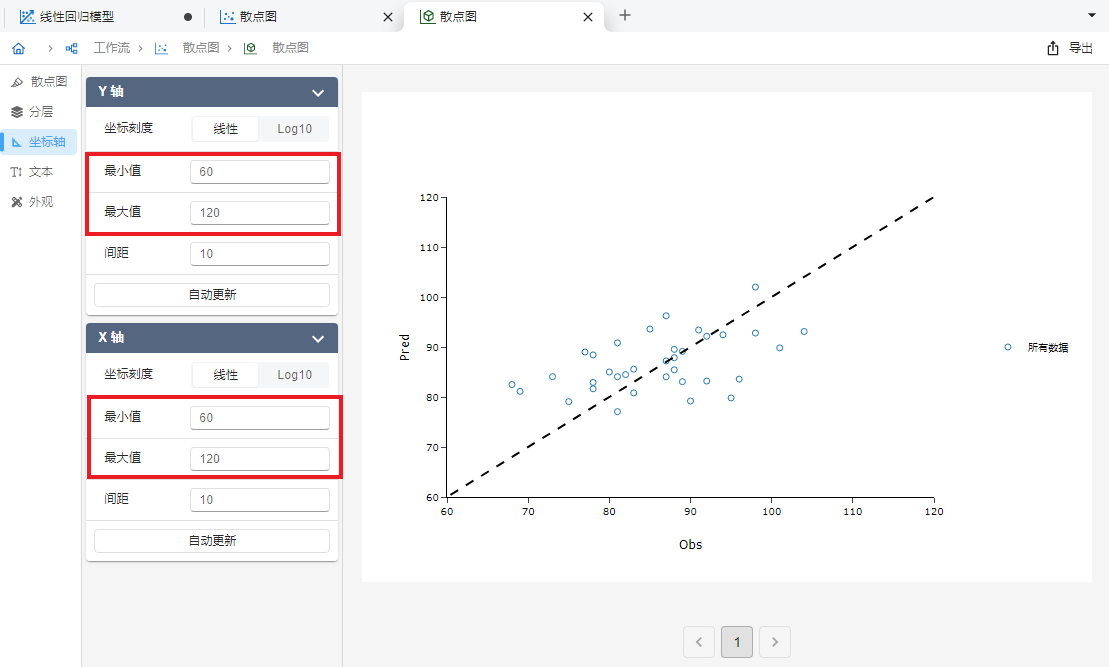
图 5.80 修改坐标轴范围示意图#
